NCERT Solution For Class 10, Maths, Chapter 6 Triangles, Exercise 6.5 includes day to day examples which can be solved by practicing all the basic concepts of property of triangles. Exercise 6.5 class 10 maths, chapter 6 is formula based.
Table of Contents
Toggle
Class 10, Maths, Chapter 6, Exercise 6.5 Solutions
Q.1. Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Ans: (i) Let a = 7 cm, b = 24 cm and c = 25 cm
Here the larger side is c = 25 cm (c2 = 625)
We have, a2 + b2 = 72 + 242 = 49 + 576 = 625 = c2
So, given sides are the sides of right triangle. Its hypotenuse is 25 cm.
(ii) Let a = 3 cm, b = 8 cm and c = 6 cm
Here the larger side is c= 8 cm
We have, a2 + c2 = 32 + 62 = 9 + 36 = 45 ≠ b2
So, given sides are not the sides of right triangle.
(iii) Let a = 50 cm, b = 80 cm and c = 100 cm
Here the large side is c = 100 cm
We have, a2 + b2 = 502 + 802 = 2500 + 6400 = 8900 ≠ c2
So, given sides are not the sides of right triangle.
(iv) let a = 13 cm, b = 12 cm and c = 5 cm.
Here the larger sides is a = 13 cm
We have, b2 + c2 = 122 + 52 = 144 + 25 = 169 = a2
So, given sides are the sides of right triangle. Its hypotenuse is 13 cm.
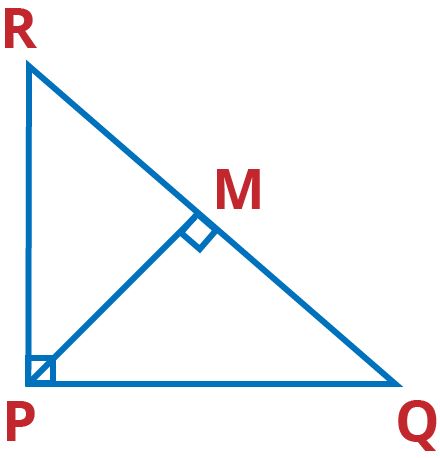
Q.2. PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM. MR
Ans:
Given: PQR is a triangle right angled at P.
PM⊥QR
To prove: PM2 = QM. MR
Proof: Since PM⊥QR
∴ ∆ PMQ ~ ∆RMP
⇒ $\frac{PM}{RM}=\frac{QR}{PM}$
⇒ PM2 = QM. MR (Hence proved)
Q.3. In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB2 = BC . BD
(ii) AC2 = BC . DC
(iii) AD2 = BD . CD
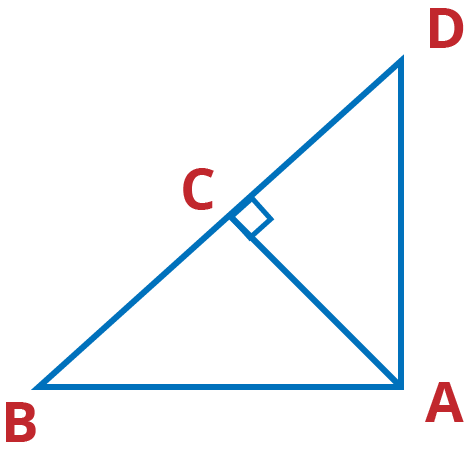
Ans:

Q.4. ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2.
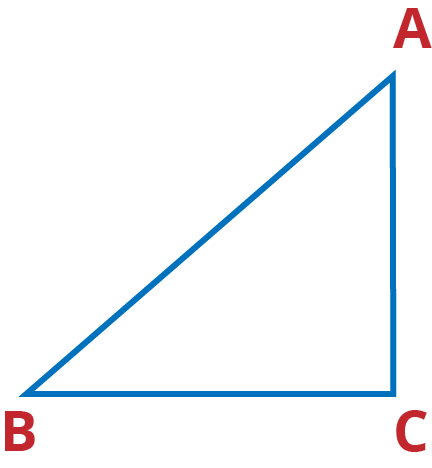
Ans: Since, ABC is an isosceles right triangle, right angled at C.
∴ AB2 = AC2 + BC2
⇒ AB2 = AC2 + AC2 [∵ BC = AC, Given]
⇒ AB2 = 2AC2
Q.5. ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Ans: Since, ABC is an isosceles right triangle with AC = BC and AB2 = 2AC2
∴ AB2 = AC2 + BC2
⇒ AB2 = AC2 + AC2 [∵ BC = AC, Given]
⇒ AB2 = AC2 + AC2
⇒ AB2 = AC2 + BC2 [∵ AC = BC, Given]
Using converse of Pythagoras theorem
∴ ∆ABC is right angled at AC.
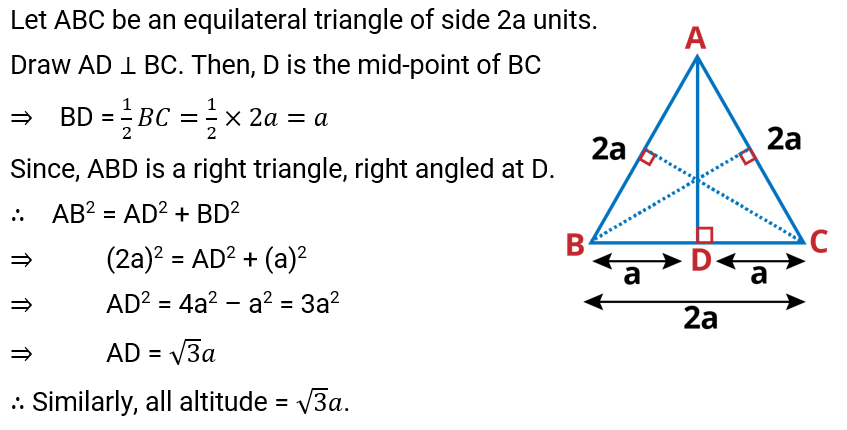
Q.6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Ans:
Q.7. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Ans:

Q.8. In Fig. 6.54, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2,
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2.
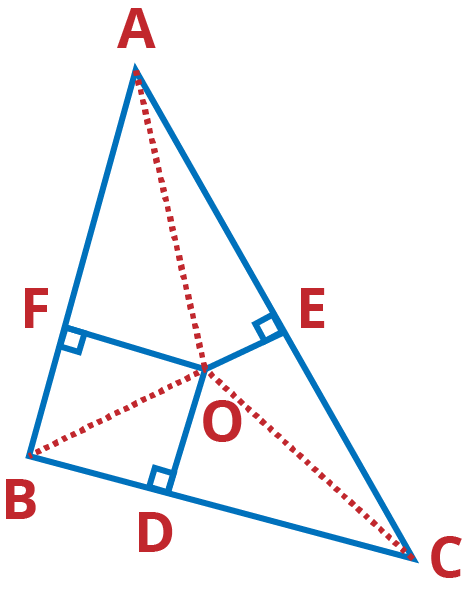
Ans: Join AO, BO and CO
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
By Pythagoras theorem, in right ∆s AFO, BOD and COE, we have
OA2 = AF2 + OF2
OB2 = OD2 + BD2
And, OC2 = CE2 + OE2
Adding all these, we get
⇒ OA2 + OB2 + OC2 = AF2 + OF2 + OD2 + BD2 + CE2 + OE2
⇒ OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2 (Hence proved)
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
We have proved that
AF2 + BD2 + CE2 = OA2 + OB2 + OC2 – OD2 – OE2 – OF2
By rearranging them, we get
⇒ AF2 + BD2 + CE2 = OA2 – OE2 + OB2 – OF2 + OC2 – OD2
⇒ AF2 + BD2 + CE2 = AE2 + BF2 + CD2 or
⇒ AF2 + BD2 + CE2 = AE2 + CD2+ BF2 (Hence proved)
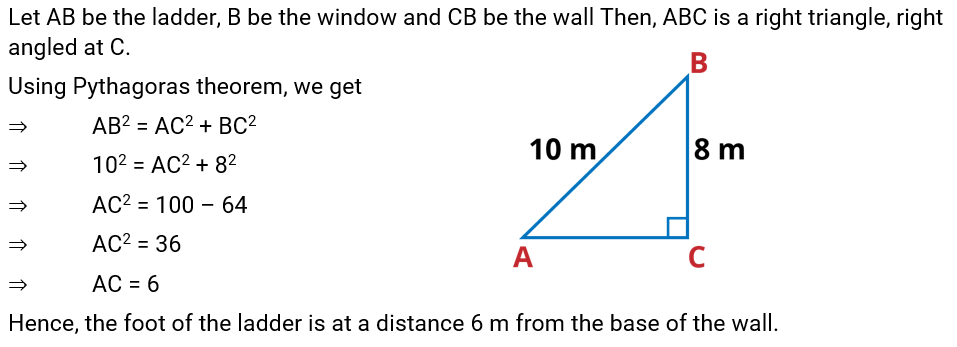
Q.9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Ans:
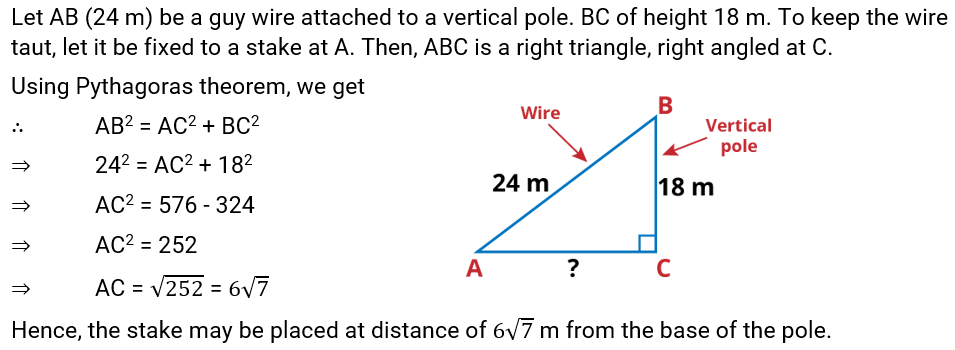
Q.10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Ans:
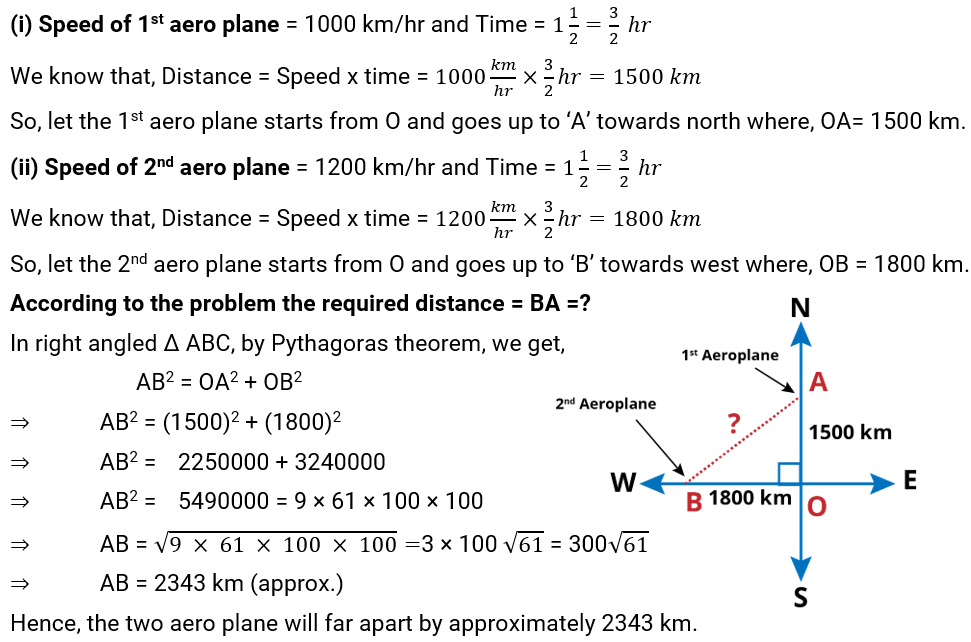
Q.11. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after hours?
Ans:
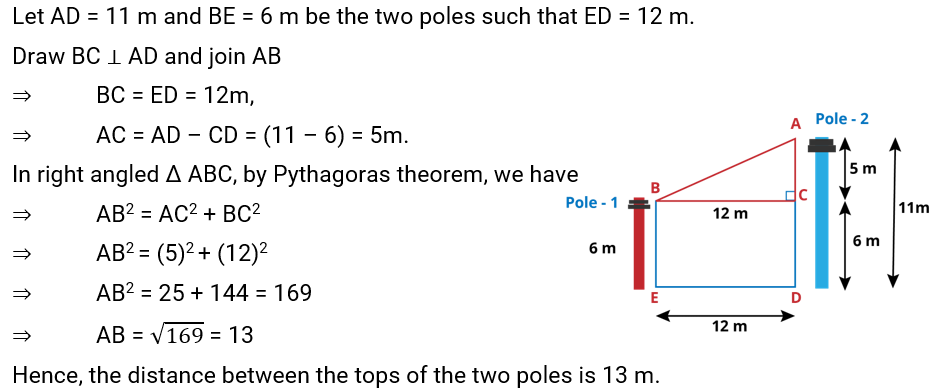
Q.12. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Ans:
Q.13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2.
Ans:

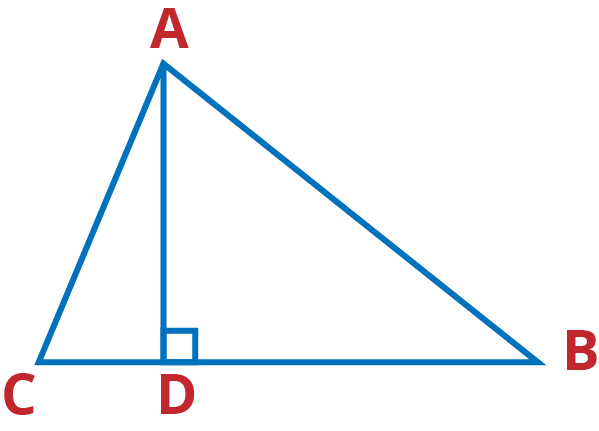
Q.14. The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD (see Fig. 6.55). Prove that 2AB2 = 2AC2 + BC2.
Ans:

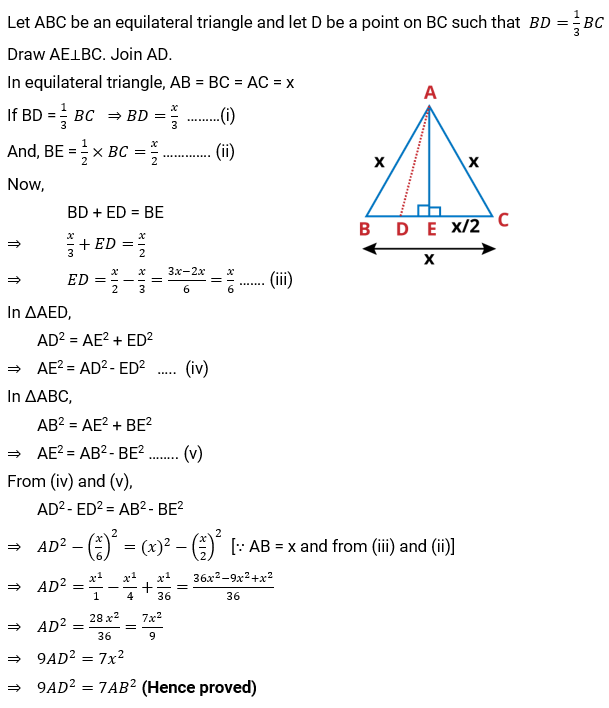
Q.15. In an equilateral triangle ABC, D is a point on side BC such that BD = $\frac{1}{3}$BC. Prove that 9 AD2 = 7 AB2.
Ans:
Q.16. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Ans:

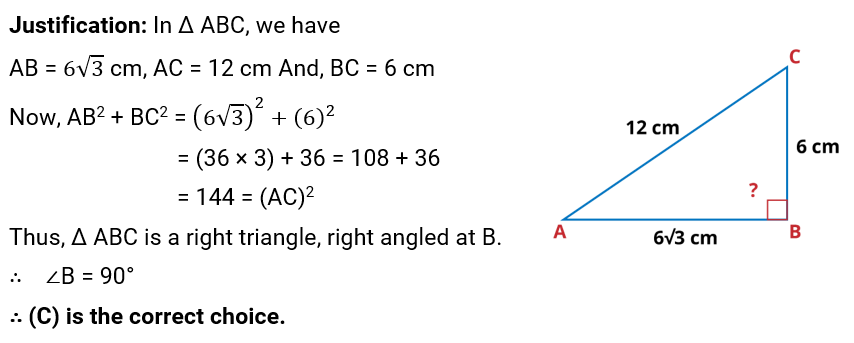
Q.17. Tick the correct answer and justify: In Δ ABC, AB = cm, AC = 12 cm and BC = 6 cm. The angle B is:
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Ans: (C) is the correct answer.