Class 10, Maths, Chapter 6, Exercise 6.6 (Optional) Solutions
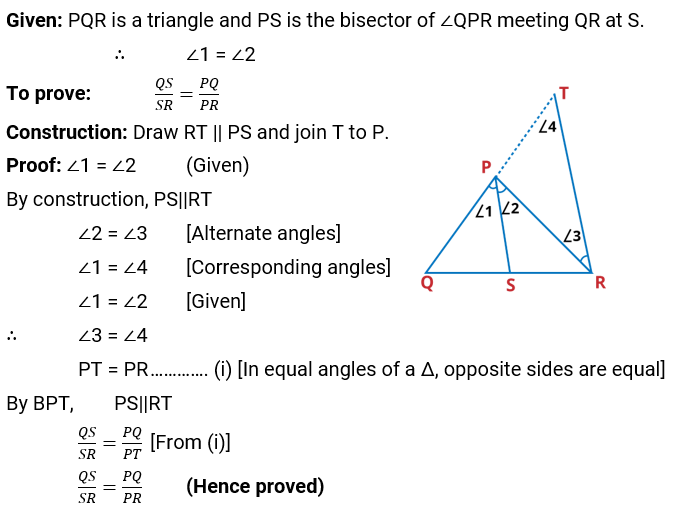
Q.1. In the given Figure, PS is the bisector of ∠QPR of Δ PQR. Prove that $\frac{QS}{SR}=\frac{PQ}{PR}$
Ans:
Q.2. In Fig. 6.57, D is a point on hypotenuse AC of Δ ABC, such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Prove that :
(i) DM2 = DN . MC
(ii) DN2 = DM . AN
Ans:
Given: We have, DM ⊥ BC and DN ⊥ AB
∴ DN||BC and DM||AB
Hence, quadrilateral BMDN is a rectangle.
DN = MB and DM = NB
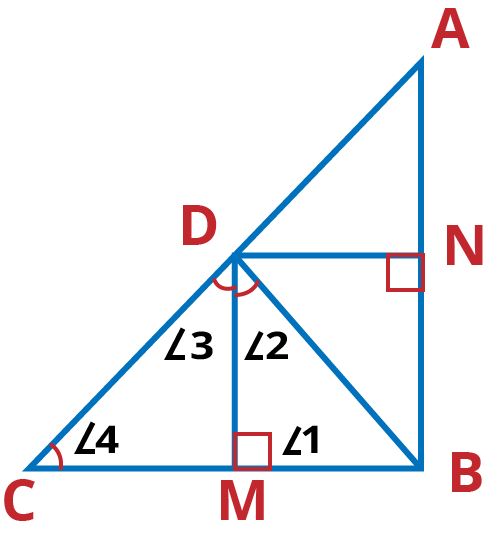
To prove: (i) DM2 = DN . MC
Proof: BD ⊥ AC [∠CDB = 900]
∠2 + ∠3 = 900 ……… (i)
In ΔCDM, we have
∠1 + ∠2 + ∠M = 1800
∠1 + ∠2 + 900 = 1800
∴ ∠1 + ∠2 = 900 ……….. (ii)
In ΔDMB, we have
∠3 + ∠6 + ∠M = 1800
∴ ∠3 + ∠6 = 900 ……….. (iii)
From (i) and (ii)
∠1 = ∠3
From (i) and (iii)
∠2 = ∠6
In ΔDCM and ΔBDM, we have
∠1 = ∠3 and ∠2 = ∠6 [by AA]
∴ Δ DCM~ΔBDM
$\frac{DM}{MB}=\frac{CM}{DM}$
DM2 = MB × MC [∵MB = DN]
DM2 = DN × MC (Hence proved)
(ii) DN2 = DM . AN
Proof: In ΔDBN, we have, ∠N = 900
∠4 + ∠7 + ∠N = 1800
∠4 + ∠7 + 900 = 1800
∴ ∠4 + ∠7 = 900 ………. (iv)
In ΔDAN, ∠N = 900
∠5 + ∠8 + ∠N = 1800
∴ ∠5 + ∠8 = 900 ………. (v)
In ΔADB, ∠D = 900
∠4 + ∠5 + ∠D = 1800
∴ ∠4 + ∠5 = 900 ………. (vi)
From (iv) and (vi)
∠7 = ∠5
From (v) and (vi)
∠4 = ∠8
In ΔDNA and ΔBND, we have
∠5 = ∠7 and ∠4 = ∠8 [by AA]
∴ Δ DNA~ΔBND
$\frac{AN}{DN}=\frac{DN}{NB}$
DN2 = AN × NB [∵NB = DM]
DN2 = AN × DM (Hence proved)
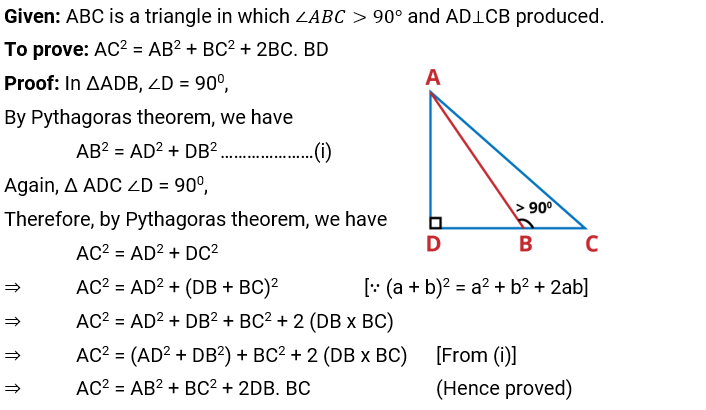
Q.3. In Figure, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2 BC . BD.
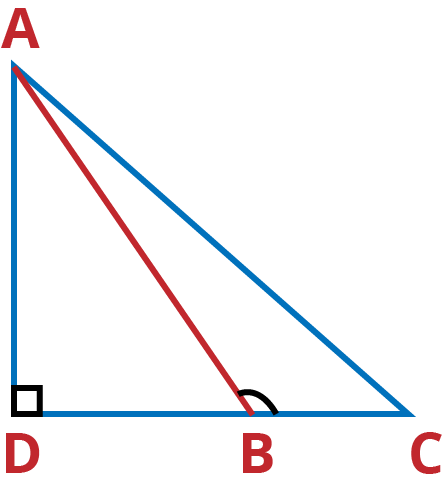
Ans:
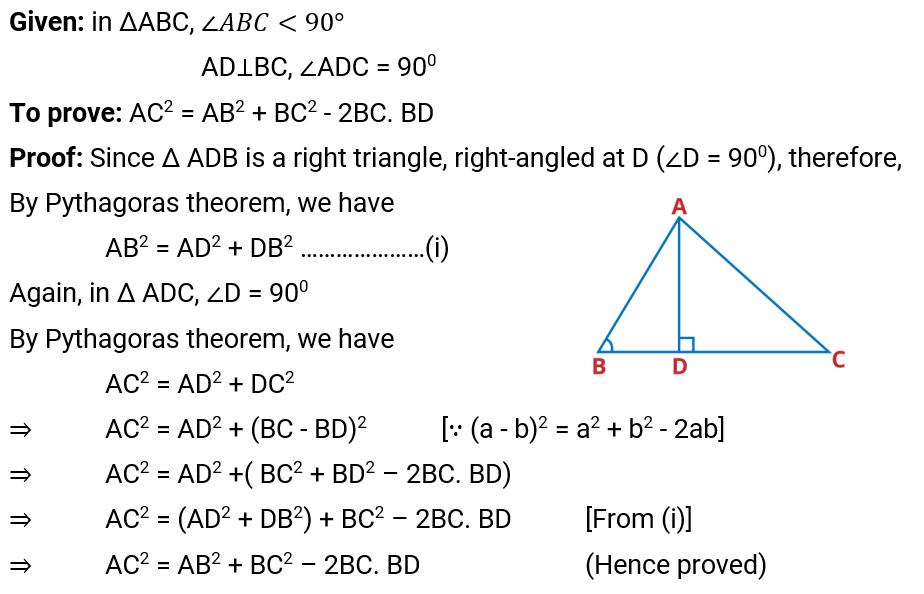
Q.4. In the given Figure, ABC is a triangle in which ∠ ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 – 2 BC . BD.
Ans:
Q.5. In Figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that :
(i) AC2 = AD2 + BC. DM + ${{\left( \frac{BC}{2} \right)}^{2}}$
(ii) AB2 = AD2 – BC. DM + ${{\left( \frac{BC}{2} \right)}^{2}}$
(iii) AC2 + AB2 = 2 AD2 + $\frac{1}{2}B{{C}^{2}}$
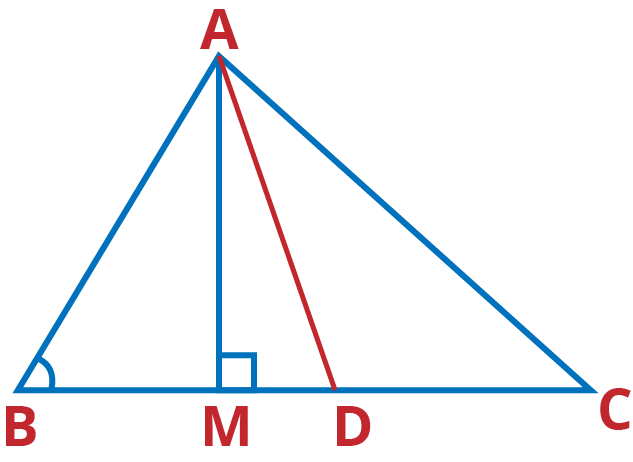
Ans:
Q.6. Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Ans:
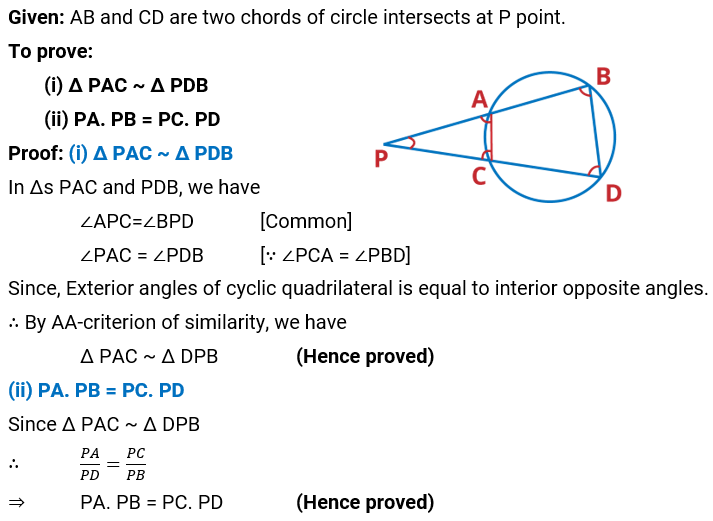
Q.7. In the given figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) Δ APC ~ Δ DPB
(ii) AP . PB = CP . DP
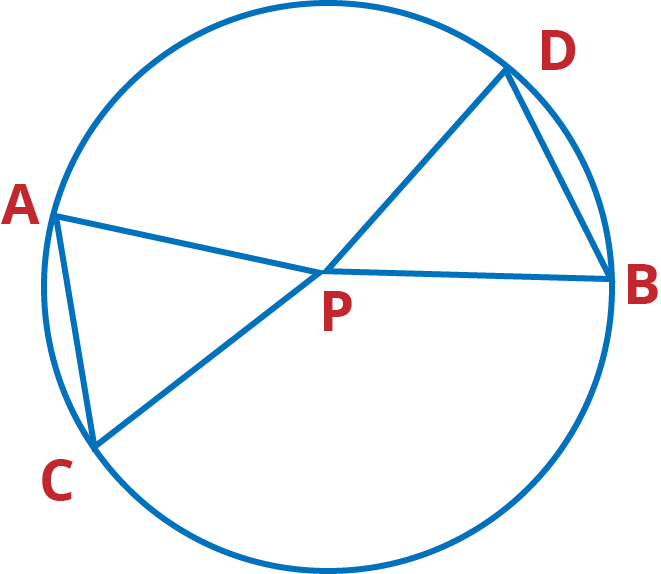
Ans:
Q.8. In Figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) Δ PAC ~ Δ PDB
(ii) PA . PB = PC . PD
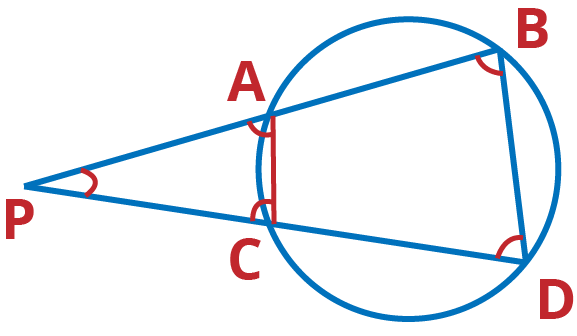
Ans:
Q.9. In Fig. 6.63, D is a point on side BC of Δ ABC such that $\frac{BD}{CD}=\frac{AB}{AC}$. Prove that AD is the bisector of ∠ BAC.
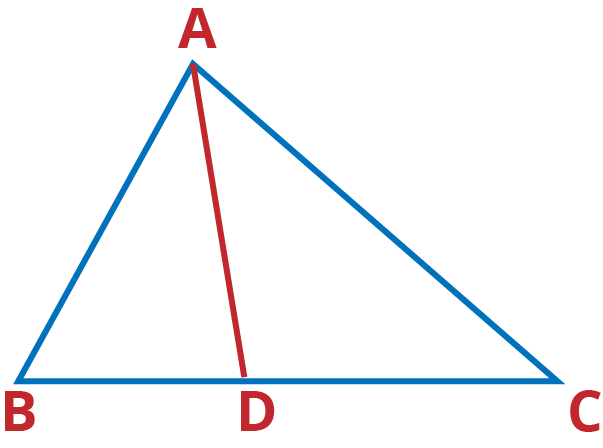
Ans:
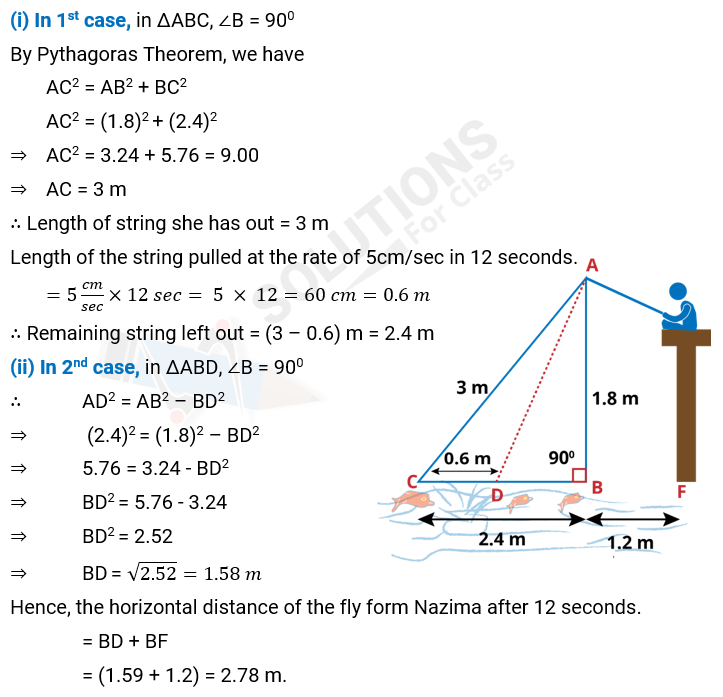
Q.10. Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out ? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
Ans:
