NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1

NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1, first we will learn how to divide the line segment and then find properties of triangles. Class 10 maths, Chapter 11, Ex. 11.1 contains total seven questions to study which are given below.  

NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1

Class 10, Maths, Chapter 11, Exercise 11.1, Solutions

In each of the following, give the justification of the construction also:

Q.1. Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.

Ans:

NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1 Q. 1

Steps of construction:

  1. Draw a line segment AB = 7.6 cm.
  2. Draw an acute angle ∠BAC.
  3. Locate (5+8 = 13) points equal line segments: A1, A2, A3, A4, ……….. A13 on line AC. Where, AA1 = A1A2 = A2A3,……….= A12A13.
  4. Join A13 to B.
  5. From point A5, draw a line A5P||A13B, by making an equal angle of ∠AA13B. So, that P divides AB in the ratio 5: 8.

On measuring the two parts, we find AP = 2.9 cm and PB = 4.7 cm (approx.).

Justification:

To prove: $\frac{AB}{DB}=\frac{5}{8}$

In ∆ABA13, PA5 || BA13

∴ ∆ APA5 ~ ∆ ABA3                      [by BPT]

⇒  $\frac{AP}{PB}=\frac{A{{A}_{5}}}{{{A}_{5}}{{A}_{13}}}$  ………….. (i)

From our construction,

⇒     $\frac{AP}{PB}=\frac{5}{8}$………….. (ii)    

From (i) and (ii), we get

⇒    $\frac{AP}{PB}=\frac{5}{8}$

Hence, AP: PB = 5 : 8

Q.2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are $\frac{2}{3}$of the corresponding sides of the first triangle.

Ans:

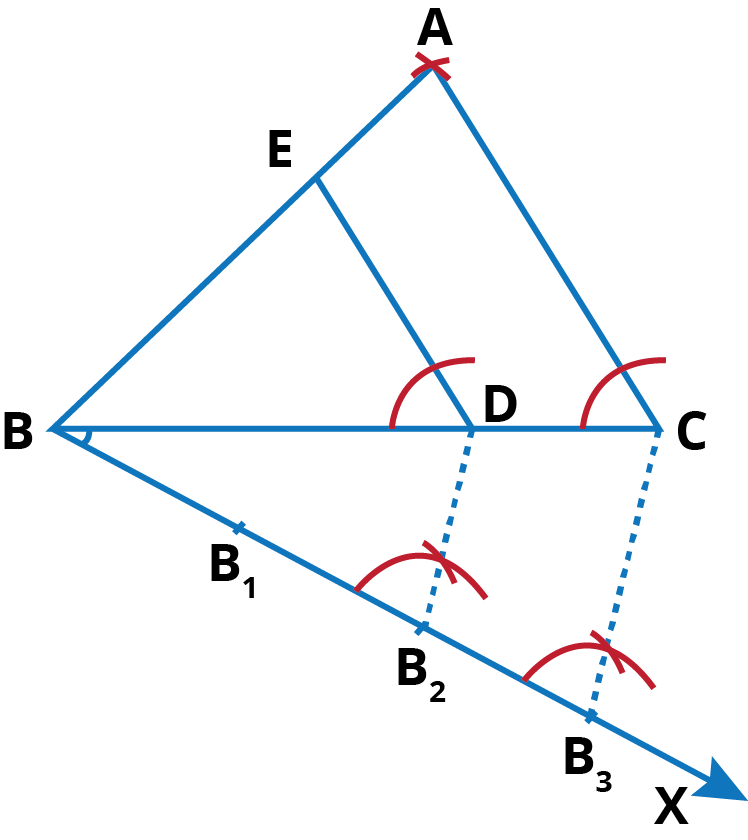
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1 Q. 2

Steps of Construction:

  1. Draw a line segment BC = 7 cm.
  2. Draw a ΔABC in which AB = 5 cm and AC = 4 cm and BC = 7 cm.
  3. below BC, make an acute angle ∠CBX.
  4. Along BX, mark off three points: B1, B2 and B3 that BB1 = B1B2 = B2B3.
  5. Join B3C.
  6. From B2, draw B2D || B3C, meeting BC at D.
  7. From D, draw ED || AC, meeting BA at E. then, EBD is the triangle whose sides are 2/3rd of the corresponding sides of ∆ ABC.

Justification: $\frac{BD}{BC}=\frac{BE}{AB}=\frac{ED}{AC}=\frac{2}{3}$

By construction,

       Since, DE || CA

         ∠BDE  =  ∠BCA                   [Corresponding angles]

In Δ BDE and ΔBCA

∠BDE  =  ∠BCA 

∠EBD = ∠ABC                 [common angle]    

∴    ∆ BDE ~ ∆ BCA              [By AA]

              $\frac{BD}{BC}=\frac{BE}{AB}=\frac{ED}{AC}$……. (i)

In ΔBB2D and ΔBB3C

Since, B2D || B3C

                 ∠BB2D = ∠BB3C       [Corresponding angles] 

                 ∠DBB2 = ∠CBB3        [common angle]

So, ΔBB2D ~ ΔBB3C  [by AA]

             $\frac{BD}{BC}=\frac{B{{B}_{2}}}{B{{B}_{3}}}=\frac{2}{3}$……………. (ii) From (i) and (ii)

             $\frac{BD}{BC}=\frac{BE}{AB}=\frac{ED}{AC}=\frac{2}{3}$             (Hence proved)

Hence, we get the new triangle similar to the given triangle whose sides are equal to $\frac{2}{3}$ rd of the corresponding sides of ∆ ABC.

Q.3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are $\frac{7}{5}$ of the corresponding sides of the first triangle.

Ans: Steps of Construction:

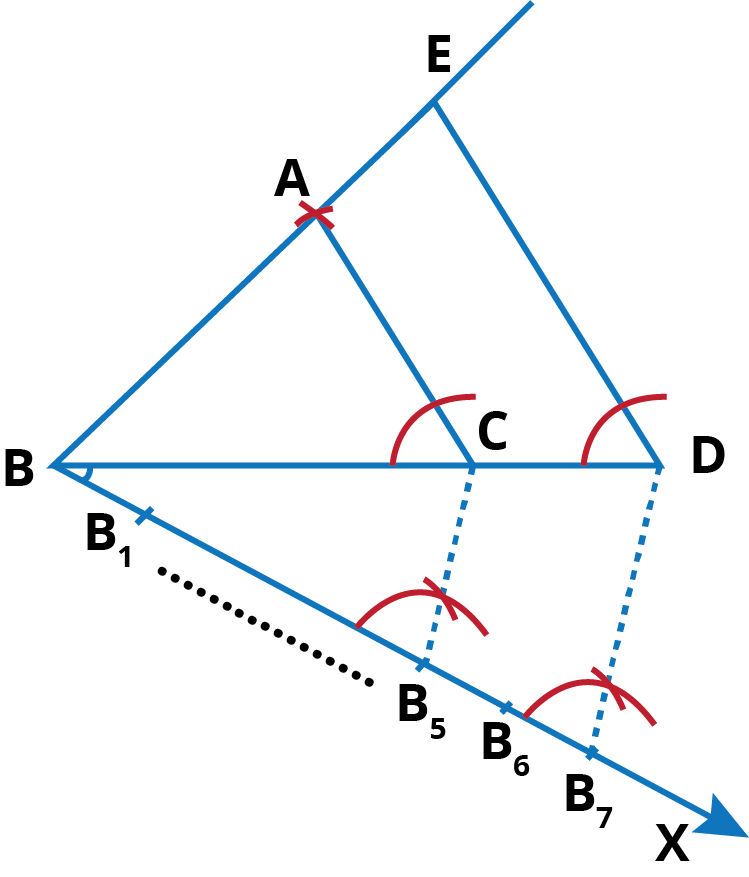
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1 Q. 3

  1. With the given data, construct ∆ ABC in which BC = 7 cm, CA = 4 cm and AB = 5 cm.
  2. Below BC, make an acute ∠CBX.
  3. Along BX, mark off seven points: B1, B2, B3, B4, B5, B6 and B7 such that BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7.
  4. Join B5C
  5. From B7, draw B7D || B5C, meeting BC produced at D.
  6. From D, draw DE || CA, meeting BA produced at E. then, EBD is the required triangle whose sides are 7/5th of the corresponding sides of ∆ABC.

Justification:

$\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}=\frac{7}{5}$

By construction,

       Since, DE || CA

∠BDE  =  ∠BCA                   [Corresponding angles]

In Δ BCA and ΔBDE

∠BCA = ∠BDE

∠ABC = ∠EBD              [common angle]

∴ ΔBCA ~ ΔBDE        [By AA]

$\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}$…….(i)

In ΔBB5C and ΔBB7D

       Since, B5C || B7D

∠BB5C = ∠BB7D                  [Corresponding angles]

∠CBB5 = ∠DBB7                   [common angle]

So, ΔBB5C ~ ΔBB7D         [By AA]

         $\frac{BD}{BC}=\frac{B{{B}_{7}}}{B{{B}_{5}}}=\frac{7}{5}$…………. (ii)

From (i) and (ii)

         $\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}=\frac{7}{5}$ (Hence proved)

Hence, we get the new triangle similar to the given triangle whose sides are equal to ${{\left( \frac{7}{5} \right)}^{rd}}$ of the corresponding sides of ∆ ABC.

Q.4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are $1\frac{1}{2}$ times the corresponding sides of the isosceles triangle.

Ans: Step of Construction:

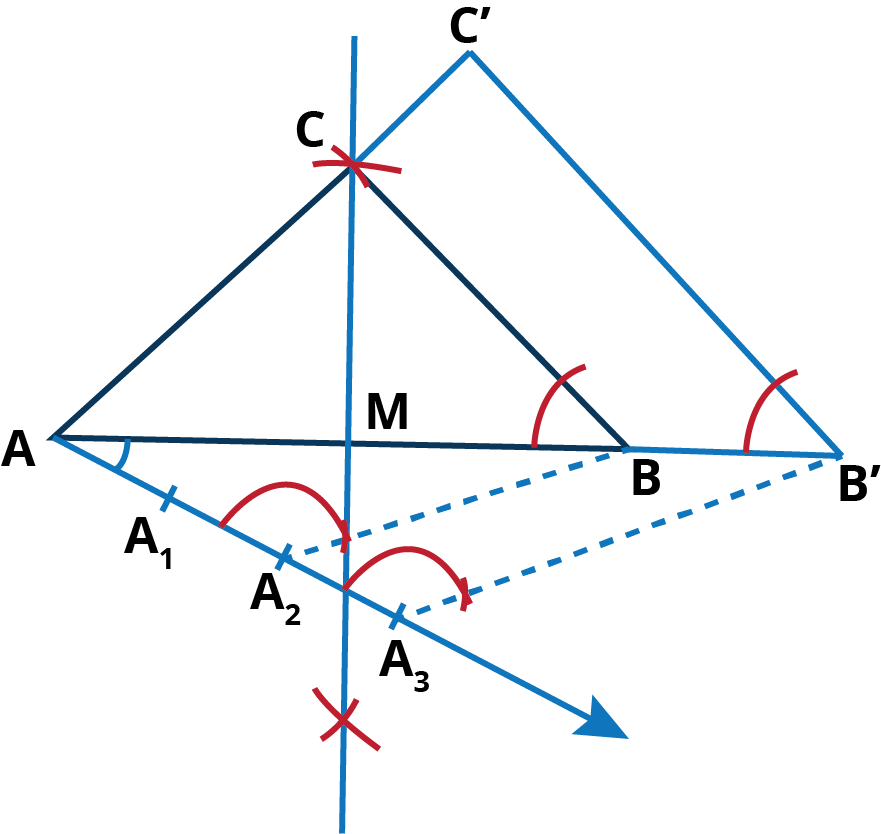
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1 Q. 4

Draw BC = 8 cm.

  1. Construct PQ, the perpendicular bisector of line segment AB at M.
  2. Along MP, cut off MA = 4 cm.
  3. Join AC and BC. Where AC = BC.
  4. draw an acute angle ∠BAA3.
  5. locate 3 point A1, A2, A3. Where, AA1 = AA2 = AA3.
  6. Join A2B.
  7. Draw A2B || A3B’.
  8. Draw B’C’||BC

Justification:

$\frac{AC’}{AC}=\frac{AB’}{AB}=\frac{B’C’}{BC}=1\frac{1}{2}=\frac{3}{2}$

By construction,

       Since, B’C’ || BC

∠AB’C’ = ∠ABC                    [Corresponding angles]

In ΔABC and ΔAB’C’

∠ABC = ∠AB’C’

∠CAB = ∠C’AB’                    [common angle]

∴ ΔAB’C’ ~ ΔABC             [By AA]

       $\frac{AC’}{AC}=\frac{AB’}{AB}=\frac{B’C’}{BC}$…….(i)

In ΔAA2B and ΔAA3B’

       Since, A2B || A3B’

∠AA2B = ∠AA3B’                 [Corresponding angles]

∠BAA2 = ∠B’AB3                 [common angle]

So, ΔAA3B ~ ΔAB3B’         [By AA]

        $\frac{AB’}{AB}=\frac{A{{B}_{3}}}{A{{A}_{2}}}=\frac{3}{2}$  …………. (ii)

From (i) and (ii)

                 $\frac{AC’}{AC}=\frac{AB’}{AB}=\frac{B’C’}{BC}=\frac{3}{2}$ (Hence proved)

Hence, we get the new triangle similar to the given triangle whose sides are $\frac{3}{2}$ , i.e., $1\frac{1}{2}$ times of the corresponding sides of the isosceles ∆ABC.

Q.5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ ABC = 60°. Then construct a triangle whose sides are $\frac{3}{4}$ of the corresponding sides of the triangle ABC.

Ans: Steps of construction:

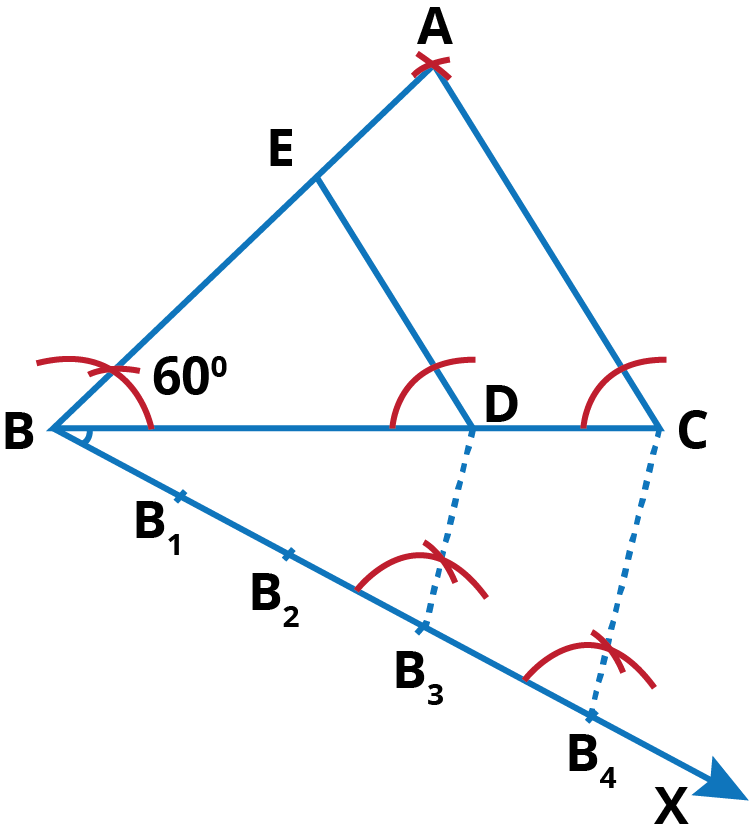
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1 Q. 5

  1. Construct ∆ ABC in which BC = 6 cm.
  2. Make an angle 600 at point B, ∠ABC = 600 .
  3. from point B take 5 cm and draw an arc to form point A.
  4. join A to C.
  5. Below BC, make an acute ∠CBX.
  6. Along BX, mark off 4 points: B1, B2, B3 and B4 such that BB1 = B1B2 = B2B3 = B3B4.
  7. Join B4C.
  8. Through B3 draw a B3D|| B4C by making same angle as ∠BB4C.
  9. From D, draw ED || CA, meeting BA at E. then, EBD is the required triangle whose sides are $\frac{3}{4}$th of the corresponding sides of ∆ABC.

 Justification:

$\frac{BD}{BC}=\frac{BE}{AB}=\frac{ED}{AC}=\frac{3}{4}$

By construction,

Since, DE || CA

∠BDE = ∠BCA                      [Corresponding angles]

In Δ BDE and ΔBCA

∠BDE = ∠BCA

∠EBD = ∠ABC                 [common angle]

∴   ∆ BDE ~ ∆ BCA               [By AA]

$\frac{BD}{BC}=\frac{BE}{AB}=\frac{ED}{AC}$……. (i)

In ΔBB3D and ΔBB4C

Since, B3D || B4C

∠BB3D = ∠BB4C       [Corresponding angles]

∠DBB3 = ∠CBB4        [common angle]

So, ΔBB2D ~ ΔBB3C  [by AA]

$\frac{BD}{BC}=\frac{B{{B}_{3}}}{B{{B}_{4}}}=\frac{3}{4}$……………. (ii)

From (i) and (ii)

$\frac{BD}{BC}=\frac{BE}{AB}=\frac{ED}{AC}=\frac{3}{4}$             (Hence proved)

Hence, we get the new triangle similar to the given triangle whose sides are equal to ${{\left( \frac{3}{4} \right)}^{rd}}$of the corresponding sides of ∆ ABC.

Q.6. Draw a triangle ABC with side BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Then, construct a triangle whose sides are   $\frac{3}{4}$ times the corresponding sides of Δ ABC.

Ans: Step of Construction:

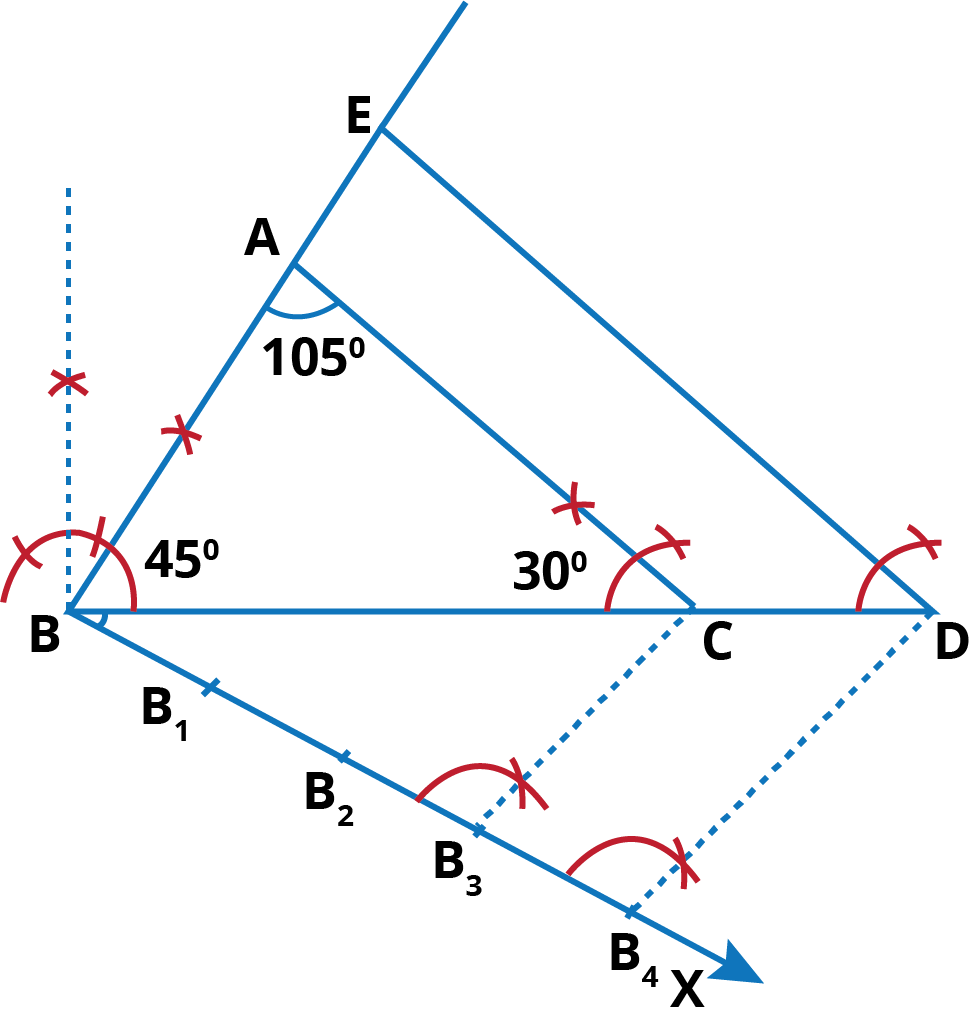
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1 Q. 6

  1. Construct ∆ ABC in which BC = 7 cm, ∠B = 450, ∠C = 1800 – (∠A+∠B)

⇒   ∠C = 180° – (105°+45°) = 180° – 150° = 30°

  1. Below BC, make an acute ∠CBX.
  2. Along BX, mark off 4 points: B1, B2, B3 and B4 such that BB1 = B1B2 = B2B3 = B3B4.
  3. Join B3C.
  4. From B4, draw B4D || B3C, meeting BC produced at D. by making same angle as ∠BB3C.
  5. From D, draw ED || CA, meeting BA at E. then, EBD is the required triangle whose sides are th times of the corresponding sides of ∆ABC.

Justification:

       $\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}=\frac{4}{3}$

By construction,

       Since, DE || CA

∠BDE = ∠BCA                      [Corresponding angles]

In Δ BCA and ΔBDE

∠BCA = ∠BDE

∠ABC = ∠EBD              [common angle]

∴ ΔBCA ~ ΔBDE        [By AA]

$\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}$…….(i)

In ΔBB3C and ΔBB4D

       Since, B3C || B4D

∠BB3C = ∠BB4D                  [Corresponding angles]

∠CBB3 = ∠DBB4                  [common angle]

So, ΔBB3C ~ ΔBB4D         [By AA]

         $\frac{BD}{BC}=\frac{B{{B}_{4}}}{B{{B}_{3}}}=\frac{4}{3}$…………. (ii)

From (i) and (ii)

         $\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}=\frac{4}{3}$         (Hence proved)

Hence, we get the new triangle similar to the given triangle whose sides are equal to ${{\left( \frac{4}{3} \right)}^{rd}}$of the corresponding sides of ∆ ABC.

Q.7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are  times the corresponding sides of the given triangle.

Ans:

 Steps of Construction:

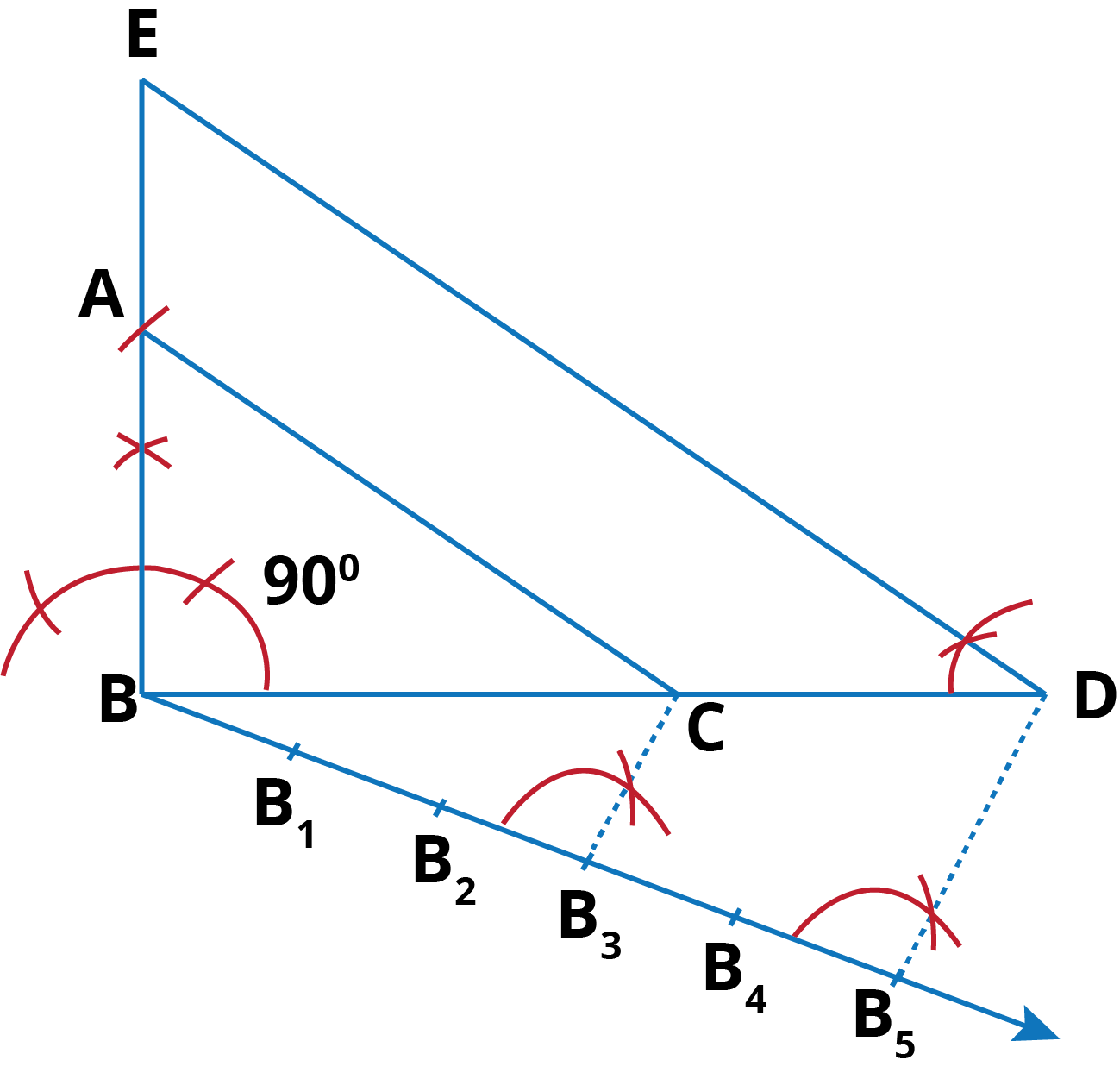
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.1 Q. 7

 

  1. Construct ∆ABC in which BC = 4 cm, ∠B = 900, BA = 3 cm
  2. construct a line BC = 4 cm.
  3. Make an angle 900 at B and take 3cm to draw an arc where AB = 3 cm.
  4. join AC.
  5. Below BC, make an acute ∠CBX.
  6. Along BX, mark off 5 points: B1, B2, B3, B4 and B5 such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
  7. Join B3C.
  8. From B5, draw B5D || B3C, meeting BC produced at D.
  9. From D, draw ED || CA, meeting BA at E. then, EBD is the required triangle whose sides are th times of the corresponding sides of ∆ABC.

Justification:

$\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}=\frac{5}{3}$

By construction,

       Since, DE || CA

∠BDE  =  ∠BCA                   [Corresponding angles]

In Δ BCA and ΔBDE

∠BCA = ∠BDE

∠ABC = ∠EBD              [common angle]

∴ ΔBCA ~ ΔBDE        [By AA]

$\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}$…….(i)

In ΔBB3C and ΔBB5D

       Since, B3C || B5D

∠BB3C = ∠BB5D                  [Corresponding angles]

∠CBB3 = ∠DBB5                  [common angle]

So, ΔBB3C ~ ΔBB5D         [By AA]

         $\frac{BD}{BC}=\frac{B{{B}_{5}}}{B{{B}_{3}}}=\frac{5}{3}$…………. (ii)

From (i) and (ii)

         $\frac{EB}{AB}=\frac{BD}{BC}=\frac{DE}{CA}=\frac{5}{3}$                 (Hence proved)

Hence, we get the new triangle similar to the given triangle whose sides are equal to ${{\left( \frac{5}{3} \right)}^{rd}}$of the corresponding sides of ∆ ABC.

Class 10 , Maths, Chapter 11, Constructions (All exercise)