NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2

In  NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2, we shall discuss questions related  construction of Tangents to a Circle. Solutions of chapter 11, Exercise 11.2 is well explained which are given below. 

NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2

Class 10, Maths, Chapter 11, Exercise 11.2, Solutions

Q.1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.

Ans:

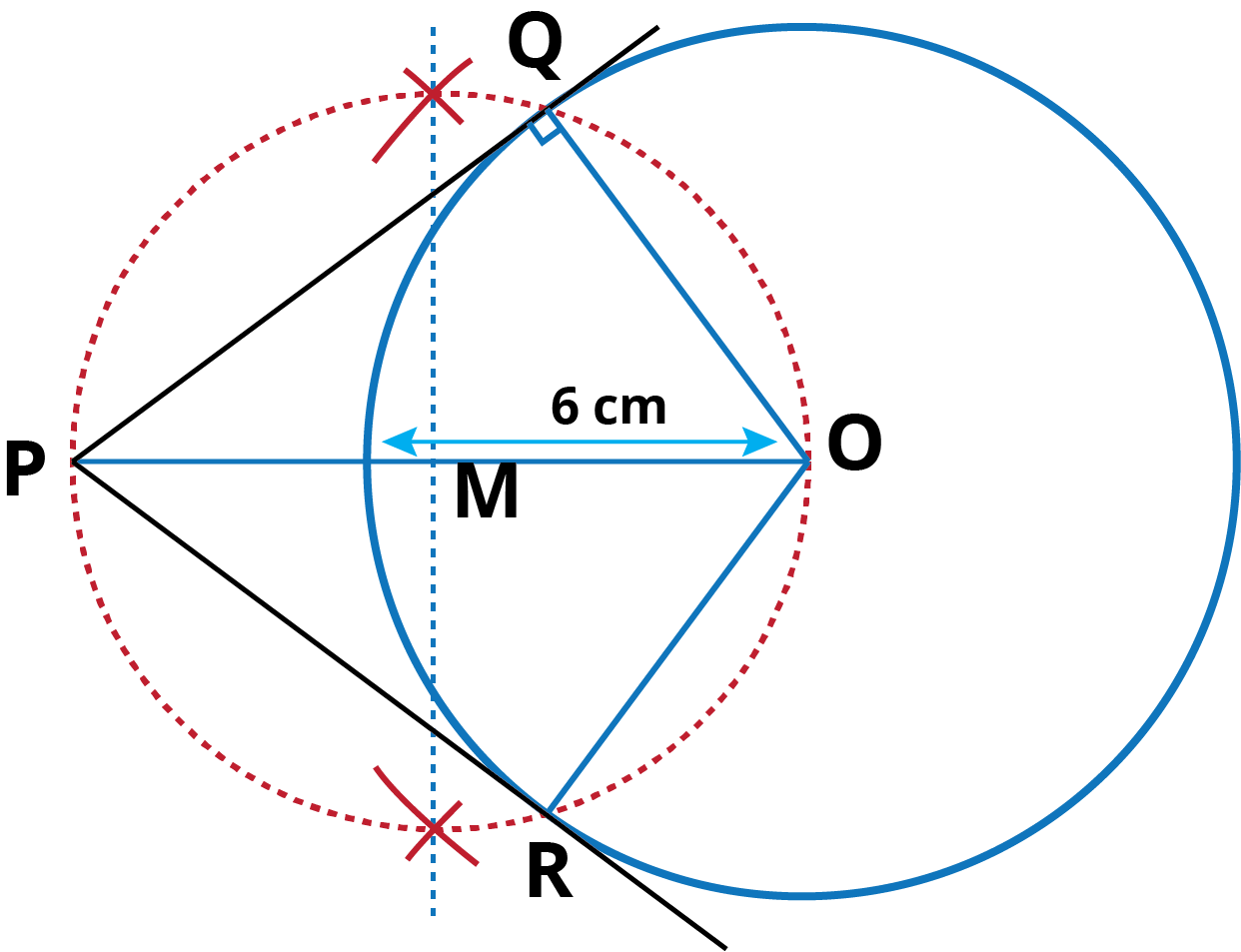
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 1

Step of Construction:

  1. Take a point O and draw a circle of radius 6 cm.
  2. Locate a point P at a distance of 10 cm from the centre O. (OP = 10 cm)
  3. Join OP and bisect it. Let M be its mid-point.
  4. With M as centre and OM as radius, draw a circle to intersect the circle at Q and R.
  5. Join PQ and PR, Then, PQ and PR are the required tangents.

On measurement, we find length of tangent 8 cm (PQ = PR = 8 cm).

Justification: To prove: PQ and PR are tangents.

On joining OQ, we find that

             ∠PQO = 90°             [Angle in the semi-circle]

∴           PQ ⊥ OQ.

Since OQ is the radius of the given circle, so PQ must be a tangent to the circle. Similarly, PR is also a tangent to the circle.

Q.2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.

Ans: Steps of Construction:                  

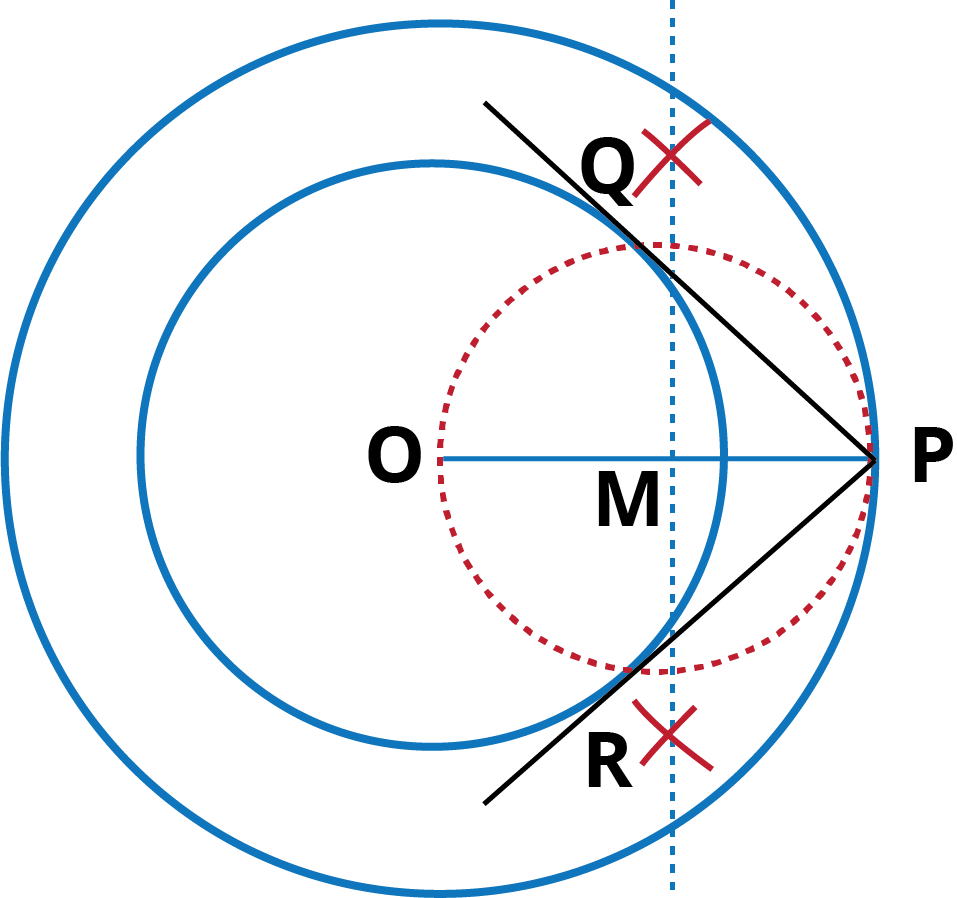
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 2

 

  1. Take a point O and draw two concentric circles of radii 4 cm and 6 cm respectively.
  2. Locate a point P on the circumference of the bigger circle.
  3. Join OP and bisect it. then M is the mid-point.
  4. With M as centre and OM as radius, draw a circle to intersect the circle at Q and R.
  5. Join PQ and PR where circle intersect.
  6. PQ and PR are the required tangents.

On measuring, we find that PQ = PR = 4.8 cm (approx.)

Justification: To prove: PQ and PR are tangents.

On joining OQ, we find that

                 ∠PQO = 90°             [Angle in the semi-circle]

∴              PQ ⊥ OQ.

Since OQ is the radius of the given circle, so PQ has to be a tangent to the circle. Similarly, PR is also a tangent to the circle.

Measurement:

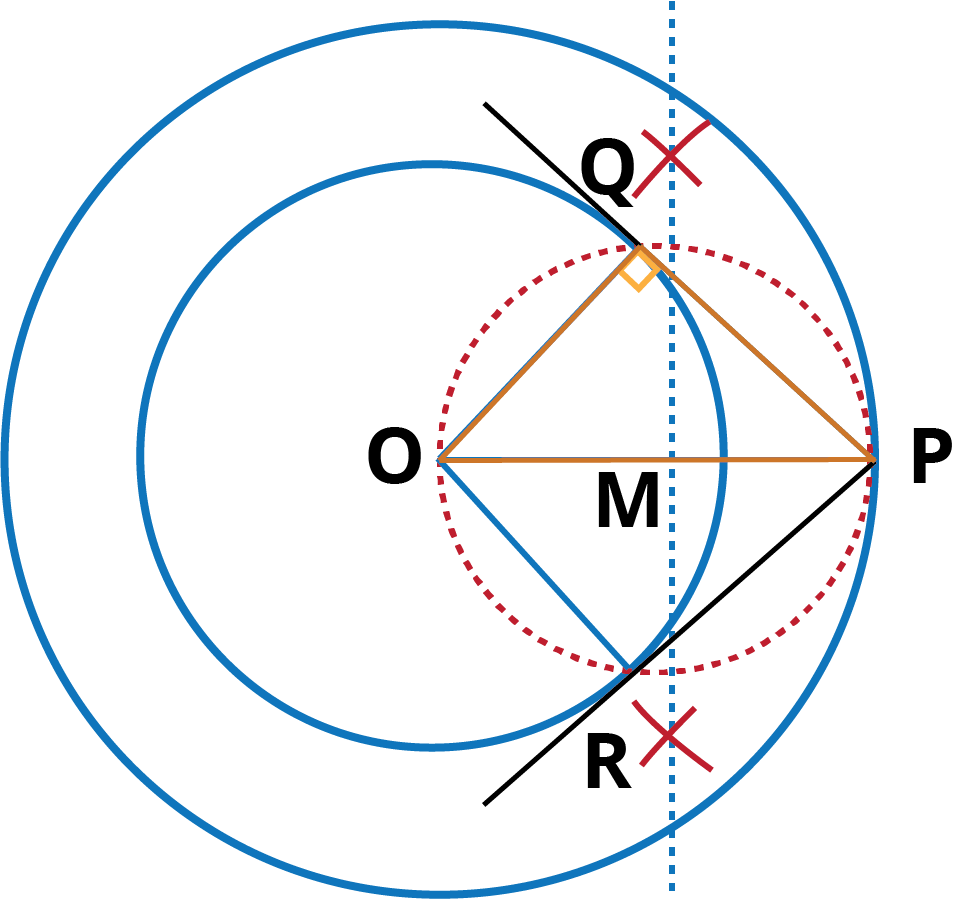
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 2

In ΔPQO, we have, OP = 6 cm and OQ = 4 cm

By using Pythagoras theorem,

⟹         (6)2 = (4)2 + PQ2 

⟹         36 = 16 + PQ2

⟹         PQ2 = 36 – 16 = 20

⟹         PQ = $\sqrt{20}$ = 4.47 cm

Hence, length of tangent is 4.47 cm.

Q.3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.

Ans:

NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 3

Steps of Construction:

  1. Take a point O, draw a circle of radium 3 cm with this point as centre.
  2. Take two points P and P’ on one of its extended diameter such that OP = OP’ = 7 cm.
  3. Bisect OP and OP’. Let their respective mid-points be M and N.
  4. With M as centre and OM as radius draw a circle to intersect the circle at Q and R and with N as centre and ON as radius draw a circle to intersect the circle at T and U.
  1. Join PQ and PR.
  2. Join P’T and P’U. now we have our required tangents.

Justification:

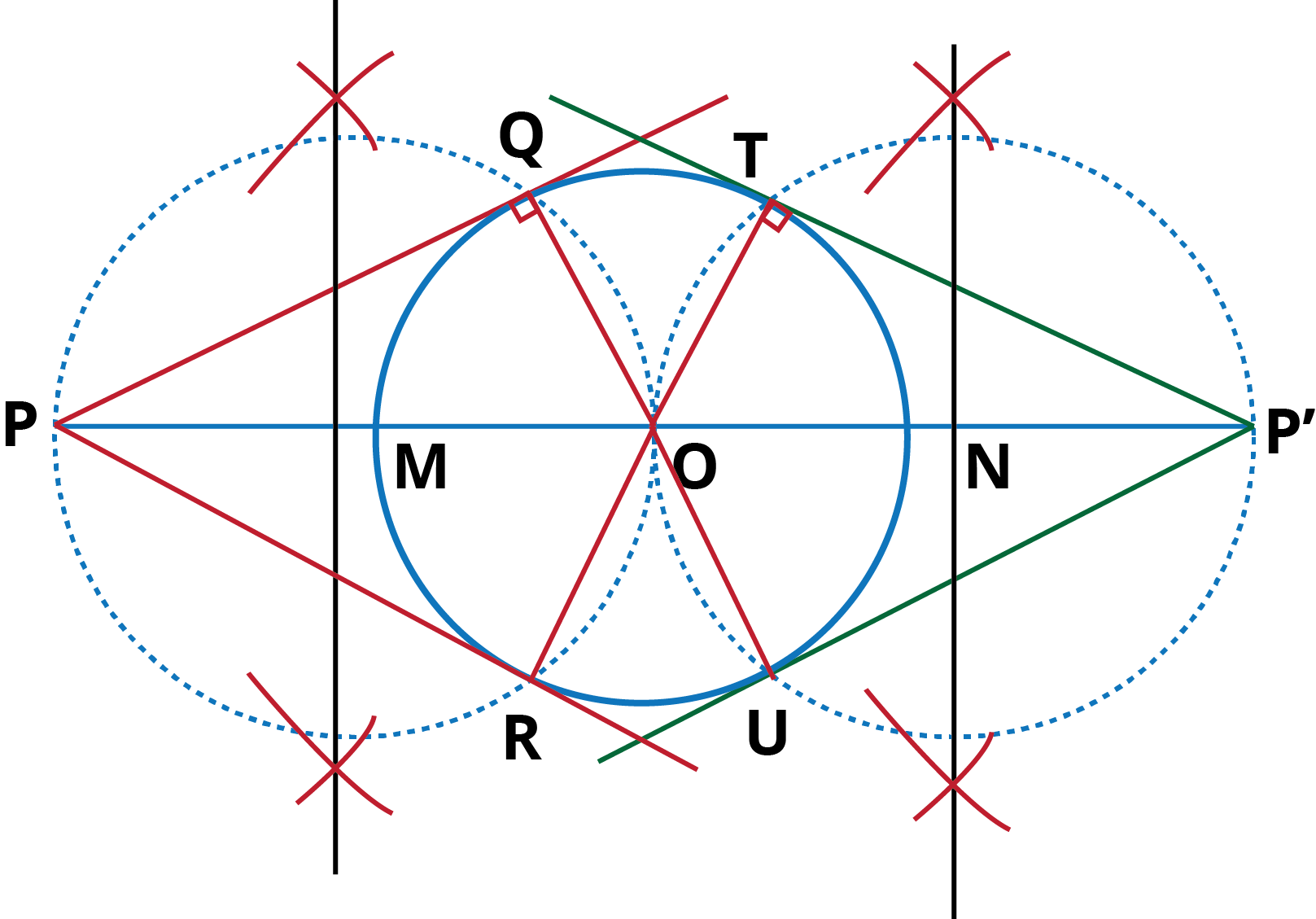
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 3

 To prove: PQ, PR, P’T and P’U are tangents.

       ∠PQO = 90°             [Angle in the semi-circle]

∴              PQ ⊥ OQ.

Since OQ is the radius of the given circle, so PQ must be a tangent to the circle. Similarly, PR, P’T and P’U are also a tangent to the circle.

Q.4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.

Ans: Steps of Construction:

NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 4

(1.) With O as centre, draw a circle of radius 5 cm.

(2.) by taking point B on circumference of circle and join OB.

(3.) Draw a radius OB and make angle 1200 (1800 – 600).

(4.) Draw any diameter AOC.

(5.) At A, draw AP ⊥ OA.

(6.) At B, draw BP ⊥ OB.

(7.) These two perpendiculars intersect each other at P.

Then, AP and BP are the required tangents.

Justification:

To prove: ∠APB = 600

Since OA is the radius, so PA has to be a tangent to the circle.

Similarly, PB is the tangent to the circle

∵     sum of angles of quadrilateral = 3600 

⟹            ∠OAP + ∠APB + ∠PBO + ∠BOA = 3600

⟹            90° + ∠APB + 90° + 180° = 3600

⟹            ∠APB = 3600 – 90° – 90° – 180°

⟹            ∠APB = 3600 – 300°

⟹            ∠APB = 600              (Hence proved)

Thus, tangents PA and PB are inclined to each other at an angle of 600.

Q.5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.

Ans: Step of Construction:

NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 5

(1.) Draw a line AB of 8 cm (AB = 8 cm).

(2.) Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw a circle of radius 3 cm.

(3.) Bisect the line AB at point O.

(4.) Clearly, O is the centre of AB. With O as centre, draw a circle of radius OA or OB, intersecting circle with centre B at T1 and T2, circle with centre A at T3 and T4.

(5.) Join AT1, AT2, BT3 and BT4. Then, these are the required tangents.

Justification:

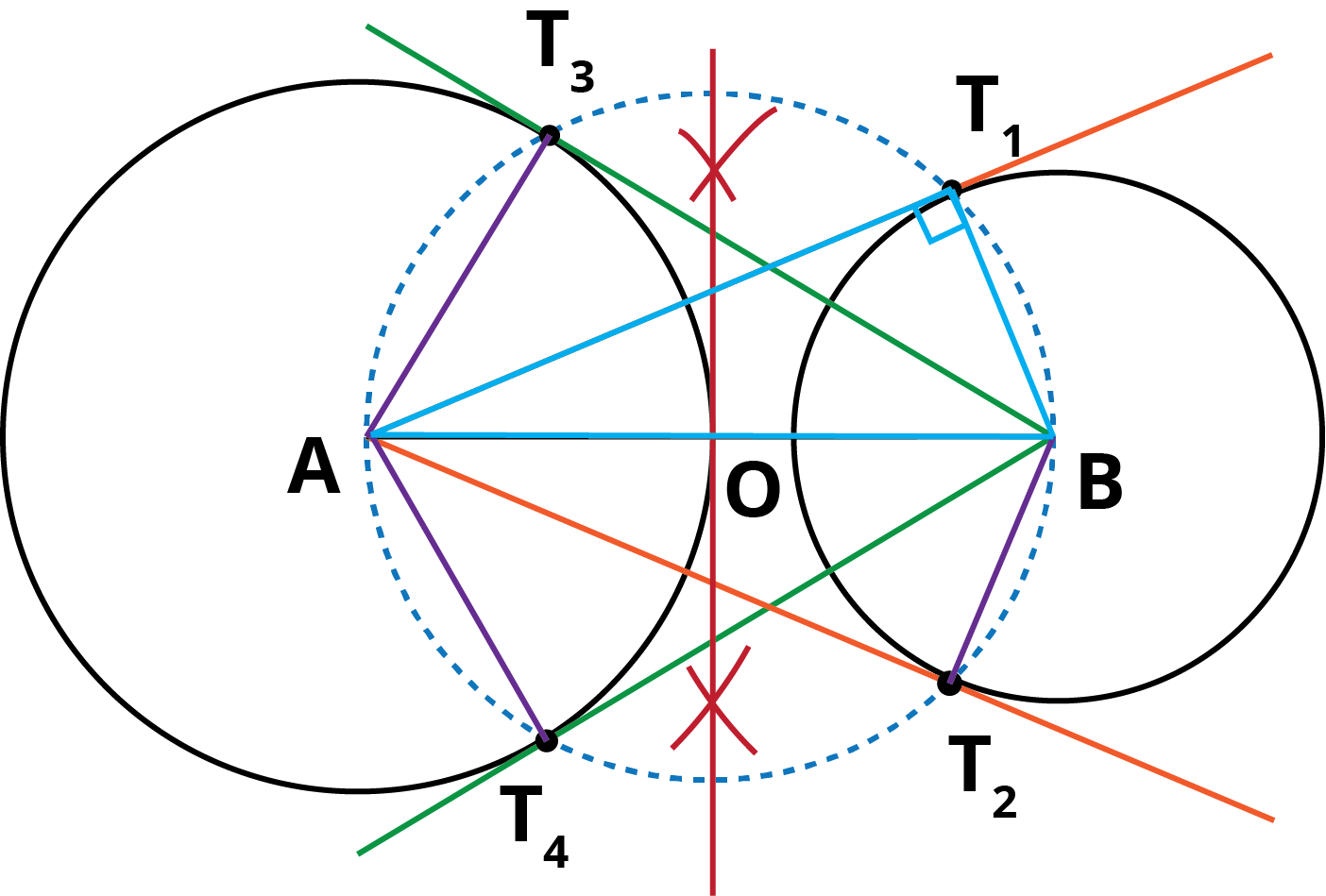
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 5

To prove: AT1, AT2 , BT3, BT4 are tangents.

On joining BT1, we find that,

                    ∠BT1A = 90°,                   [Angle in the semi-circle]

∴                    AT1 ⊥ BT1

Since BT1 is the radius of the given circle, so AT1 must be a tangent to the circle.

Similarly, AT2, BT3 and BT4 are the tangents.

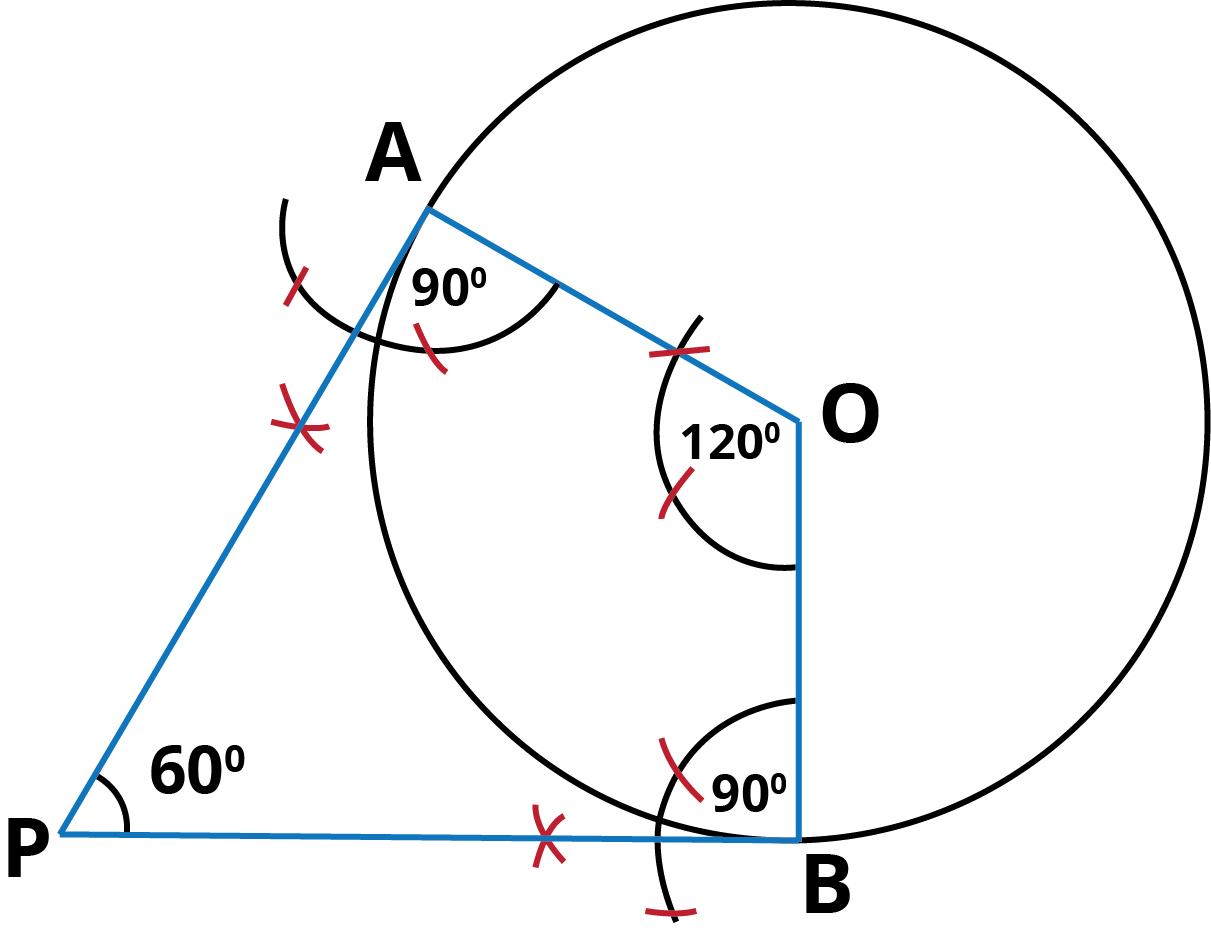
Q.6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠ B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.

Ans:

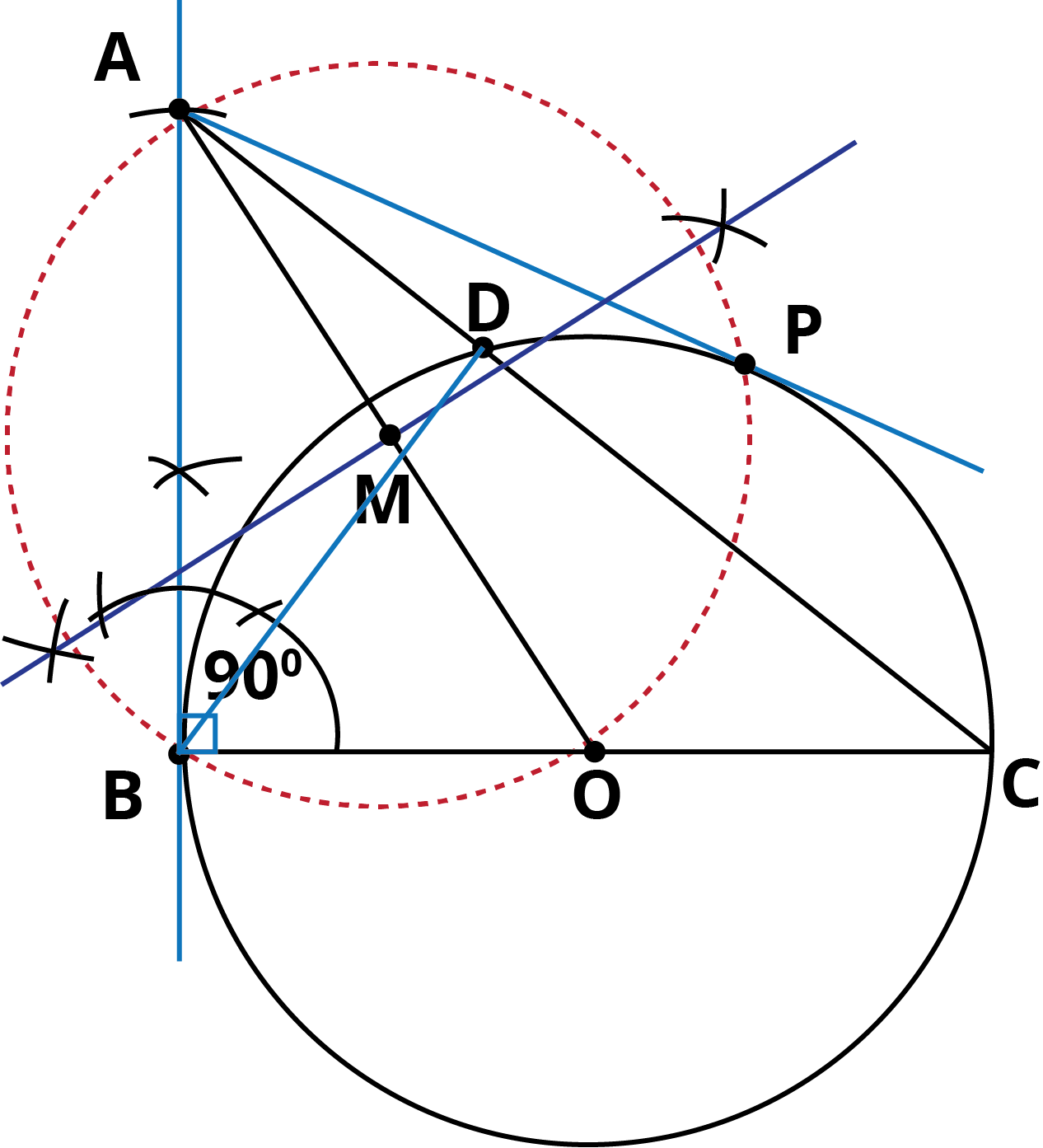
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 6

Step of Construction:              

(1.) With the given data, take a line BC of 8 cm (BC = 8cm).

(2.) taking O as centre OB as radius, draw a circle.

  1. Draw an angle of 900 at point B. draw an arc of 6 cm from point B.
  2. Join AB and AC.
  3. Join B to D where AC and circle intersect.
  4. Draw perpendicular bisector of OA. This perpendicular bisector meets OA at M.
  5. Taking M as centre and MA as radius, draw a circle which intersects the circle at P and B.
  6. Join AP and AB. These are the required tangents from A.

Justification:

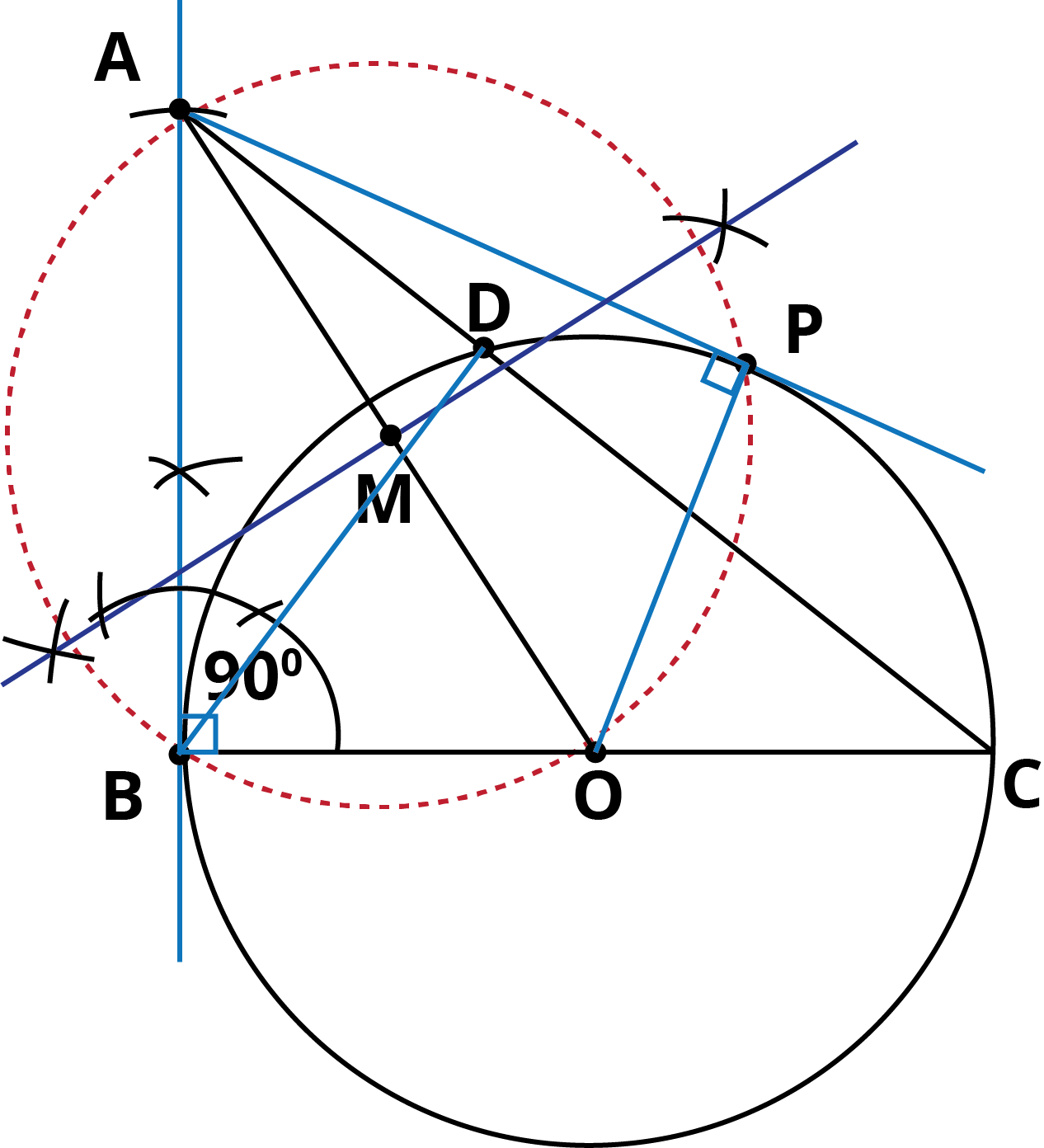
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 6

To prove: AB and AP are tangents.

On joining PO, we find that,

                    ∠APO = 90°,                    [Angle in the semi-circle]

∴                    PO ⊥ AP

Since OP is the radius of the given circle, so AP must be a tangent to the circle.

Similarly, AB is the tangent.

Q.7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.

Ans:

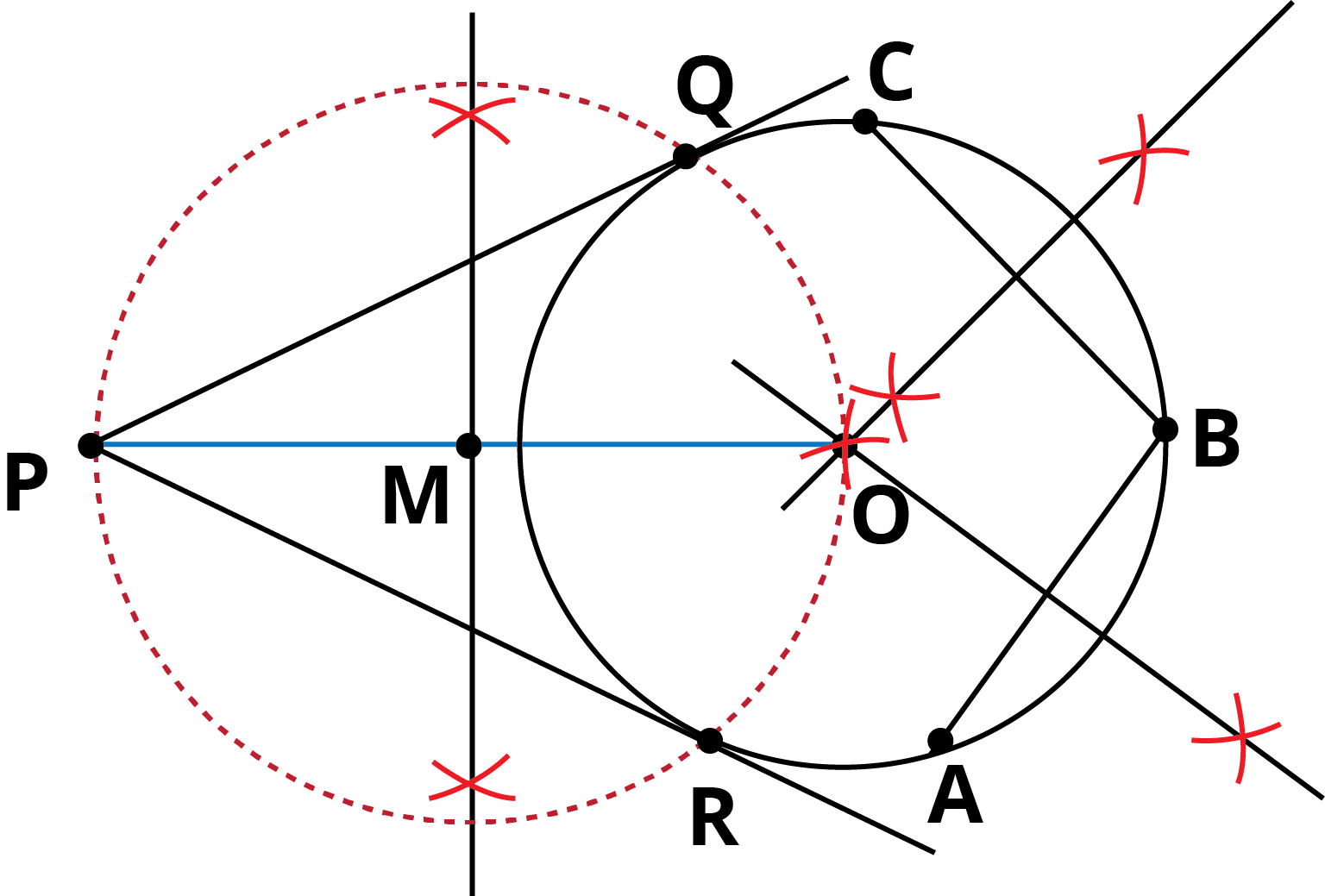
NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 7

Steps of Construction:

  1. Draw a circle with the help of a bangle.
  2. Draw two secant or chord AB and BC on the circle.
  3. Draw a bisector of AB and BC, which meets at point O consider as centre of circle.
  4. Take point P outside the circle. Join OP.
  5. Bisect OP line by making arc and this way we get out bisector at point M.
  6. Take MP as radius and M as a centre, draw a circle which intersects the circle at Q and R. Then, PQ and PR are the required tangent lines.

Justification:

NCERT Solution For Class 10, Maths, Chapter 11, Constructions, Exercise 11.2 Q. 7

To prove: PQ and PR are tangents.

On joining QO, we find that,

                    ∠OQP = 90°,                    [Angle in the semi-circle]

∴                    PQ ⊥ OQ

Since OQ is the radius of the given circle, so PQ must be a tangent to the circle.Similarly, PR is the tangent.

Class 10 , Maths, Chapter 11, Constructions (All exercise)