Understanding Elementary Shapes, Exercise 5.7

Q.1. Say True or False:

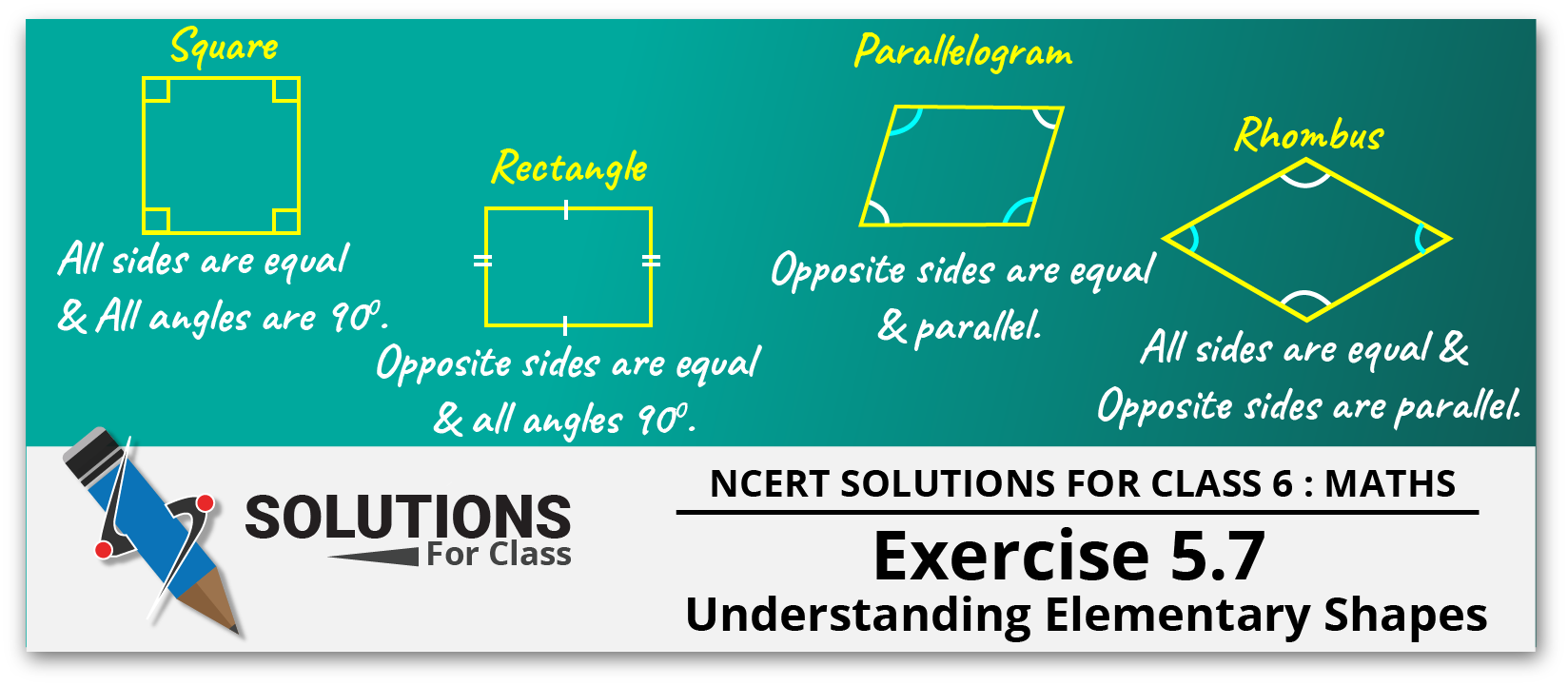
(a) Each angle of a rectangle is a right angle.

(b) The opposite sides of a rectangle are equal in length.

(c) The diagonals of a square are perpendicular to one another.

(d) All the sides of a rhombus are of equal length.

(e) All the sides of a parallelogram are of equal length.

(f) The opposite sides of a trapezium are parallel.

Ans: (a) True, each angle of a rectangle is a right angle.

(b) True, the opposite sides of a rectangle are equal in length.

(c) True, the diagonals of a square are perpendicular to one another

(d) True, all the sides of a rhombus are of equal length

(e) False, all the sides of a parallelogram are not equal

(f) False, the opposite sides of a trapezium are not parallel

Q.2. Give reasons for the following:

(a) A square can be thought of as a special rectangle.

(b) A rectangle can be thought of as a special parallelogram.

(c) A square can be thought of as a special rhombus.

(d) Squares, rectangles, parallelograms are all quadrilaterals.

(e) Square is also a parallelogram.

Ans: (a) Because a square has all the properties as that of rectangle. So, it is a special rectangle.

(b) Because its opposite sides are equal and parallel. So, it is a special parallelogram.

(c) Because its four sides are equal and diagonals are perpendicular to each other. So, it is a special rhombus.

(d) Because they are all enclosed by four sides.

(e) Because its opposite sides are equal and parallel. So, square is also a parallelogram.

 Q.3. A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?

Ans: A square is a regular quadrilateral because all the interior angles are of 90⁰ and all sides are of same length.