
Table of Contents
ToggleClass 7, Maths, Chapter 7, Exercise 7.2 Solutions
Q.1. Which congruence criterion do you use in the following?
(a) Given: AC = DF
AB = DE
BC = EF
So, ∆ABC ≅ ∆DEF
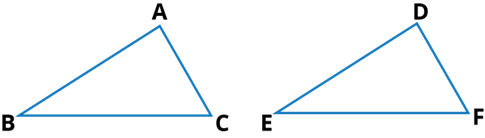
Ans:
(a) By SSS congruence property
it is given that AC = DF, AB = DE, BC = EF. Here, The three sides of one triangle are equal to the three corresponding sides of another triangle.
Therefore, ΔABC≅ ΔDEF [by SSS congruence property]
(b) Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆PQR ≅ ∆XYZ
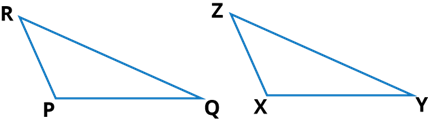
Ans: By SAS congruence property
Two triangles are congruent if the two sides and one angle in one of the triangle are equal to the corresponding sides and the included angle of the other.
Therefore, ΔACB ≅ ΔDEF
(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ∆LMN ≅ ∆GFH
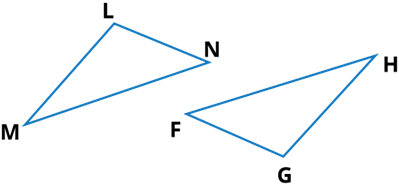
Ans: By ASA congruence property
Two triangles are congruent if the two angles and the included side of one are equal to the corresponding two angles and the included side of the other.
Therefore, ΔLMN ≅ ΔGFH
(d) Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ∆ABE ≅ ∆CDB
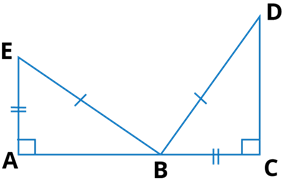
Ans: By RHS congruence property
Two right triangles are congruent if Hypotenuse and one side of a right angled triangle are respectively equal to the hypotenuse and one side of another right angled triangle.
Therefore, ΔABE ≅ ΔACD
Q.2. You want to show that ∆ART ≅ ∆PEN,
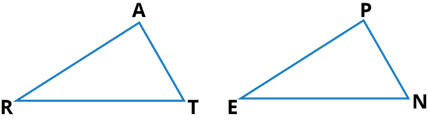
(a) If you have to use SSS criterion, then you need to show
(i) AR = (ii) RT = (iii) AT =
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and (ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ? (ii) ?
Ans:
(i) we have ∆ART ≅ ∆PEN,
By using SSS criterion,
∴ (i) AR = PE (ii) RT = EN (iii) AT = PN
(b) Given that ∠T = ∠N and by using SAS criterion,
∴ (i) RT = EN
(ii) PN = AT
(c) Given that AT = PN and by using ASA criterion,
(i) ∠ATR = ∠PNE
(ii) ∠RAT = ∠EPN
Q.3. You have to show that ∆AMP ≅ ∆AMQ. In the following proof, supply the missing reasons.
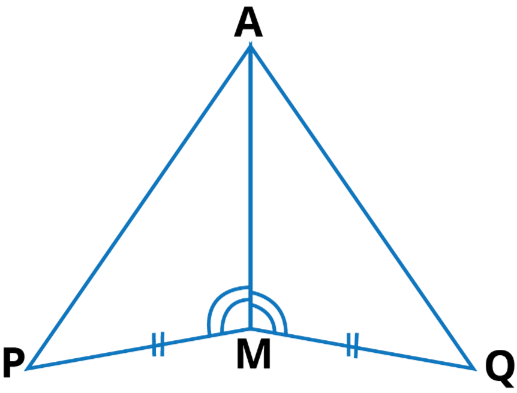
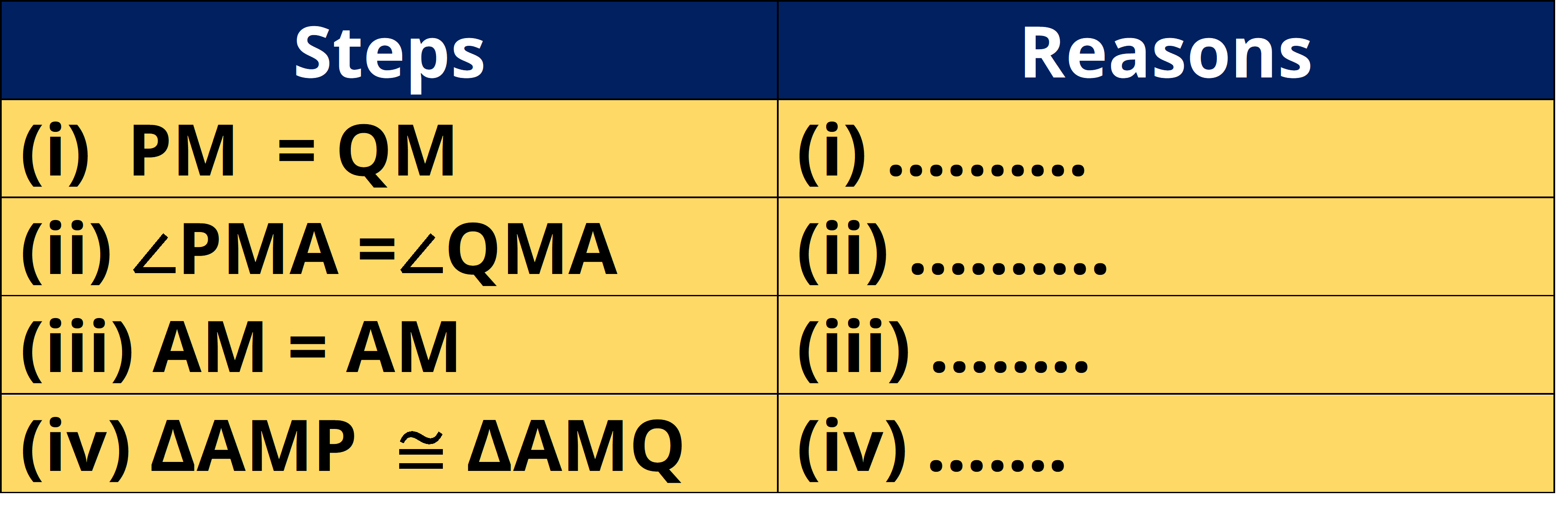
Ans:

Q.4. In ∆ABC, ∠A = 30° , ∠B = 40° and ∠C = 110° In ∆PQR, ∠P = 30° , ∠Q = 40° and ∠R = 110° A student says that ∆ABC ≅ ∆PQR by AAA congruence criterion. Is he justified? Why or why not?
Ans:
No, because the two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be enlarged copy of the other.
Q.5. In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ∆RAT ≅ ?
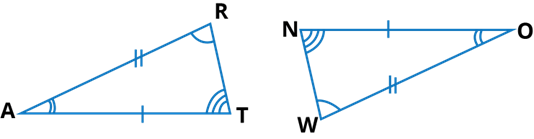
Ans:
We observe from the given figures that,
∠TRA = ∠OWN
∠TAR = ∠NOW
∠ATR = ∠ONW
Hence, ΔRAT ≅ ΔWON [By SAS congruence]
Q.6. Complete the congruence statement:
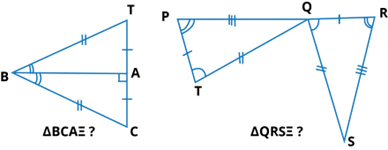
Ans:
First consider the ΔBCA and ΔBTA
From the figure, it is given that,
BT = BC BA = BA, TA = CA
Hence, ΔBCA ≅ ΔBTA [by SSS congruence rule]
Similarly,
In ΔQRS and ΔTPQ
From the figure, it is given that
PT = QR
TQ = QS
PQ = RS
Hence, ΔQRS ≅ ΔTPQ [by SSS congruence rule]
Q.7. In a squared sheet, draw two triangles of equal areas such that
(i) the triangles are congruent.
(ii) the triangles are not congruent.
What can you say about their perimeters?
Ans:
(i) The triangles are congruent
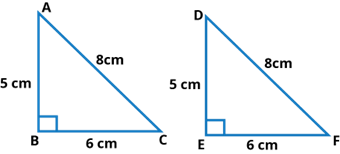
In the above figure, ΔABC and ΔDEF have equal areas.
And also, ΔABC ≅ ΔDEF [by SSS congruence rule]
So, we can say that perimeters of ΔABC and ΔDEF are equal.
(ii) when the triangles are not congruent:
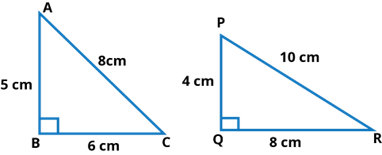
In the above figure, ΔABC and ΔPQR
ΔLMN is not congruent to ΔOPQ
So, we can also say that their perimeters are not same.
Q.8. Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Ans:
Let us draw triangles ΔPQR and ΔABC.
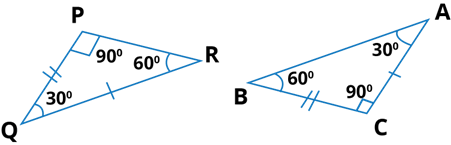
In these figures, all angles of two triangles are equal. But, out of three sides only two sides are equal. Hence, ΔPQR is not congruent to ΔABC.
Q.9. If ∆ABC and ∆PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
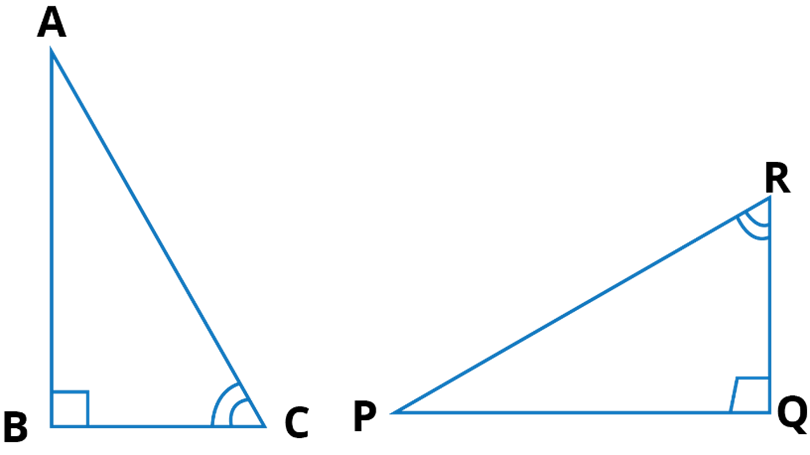
Ans:
ΔABC and ΔPQR are congruent. The other additional pair of corresponding part is BC = QR
∠ABC = ∠PQR = 90o
∠BCA = ∠PRQ
∴ ΔABC ≅ ΔPQR [By ASA congruence rule]
Q.10. Explain, why ∆ABC ≅ ∆FED.
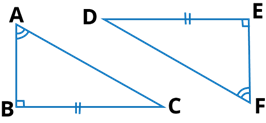
Ans:
it is given that,
∠B = ∠E = 90o
∠A = ∠F
BC = DE
By ASA congruence property,
∴ ΔABC ≅ ΔFED

