
Table of Contents
ToggleClass 7, Maths, Chapter 13, Exercise 13.1 Solutions
Q.1. Find the value of:
(i) 26
(ii) 93
(iii) 112
(iv) 54
Ans:
(i) 26 = 2 x 2 x 2 x 2 x 2 x 2 = 64
(ii) 93 = 9 x 9 x 9 = 729
(iii) 112 = 11 x 11 = 121
(iv) 54 = 5 x 5 x 5 x 5 = 625
Q.2. Express the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5× 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c × c × d
Ans:
(i) 6 × 6 × 6 × 6 = 64
(ii) t × t = t2
(iii) b × b × b × b = b4
(iv) 5 × 5× 7 × 7 × 7 = 52 x 73
(v) 2 × 2 × a × a = 22 x a2
(vi) a × a × a × c × c × c × c × d = a3 x c4 x d
Q.3. Express each of the following numbers using exponential notation:
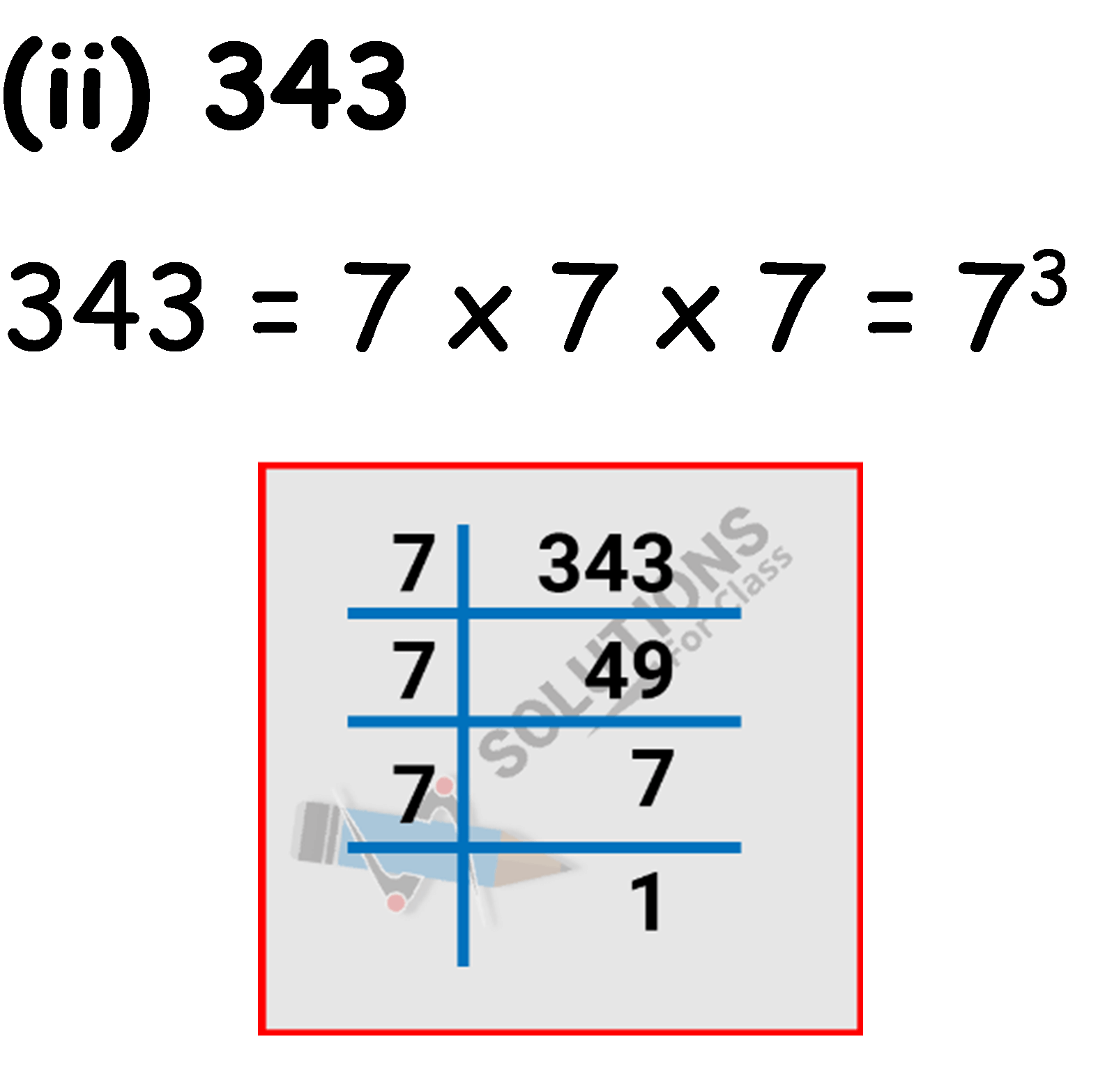
(i) 512
(ii) 343
(iii) 729
(iv) 3125



Q.4. Identify the greater number, wherever possible, in each of the following?
(i) 43 or 34
(ii) 53 or 35
(iii) 28 or 82
(iv) 1002 or 2100
(v) 210 or 102
Ans:
(i) 43 or 34
43 = 4 x 4 x 4 = 64
34 = 3 x 3 x 3 x 3 = 81
So, 64 < 81
Hence, 34 is greater than 43.
(ii) 53 or 35
53 = 5 x 5 x 5 = 125
35 = 3 x 3 x 3 x 3 x 3= 243
So, 125 < 243
Hence, 35 is greater than 53.
(iii) 28 or 82
28 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256
82 = 8 x 8 = 64
So, 256 > 64
Hence, 28 is greater than 82 .
(iv) 1002 or 2100
1002 = 100 x 100 = 10000
If we take , 210 = 2x2x2x2x2x2x2x2x2x2= 1024. Which means 2100 is very large than 1002.
So, 1002 < 2100
Hence, 2100 is greater than 1002
(v) 210 or 102
210 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 1024
102 = 10 x 10= 100
So, 210 > 102
Hence, 210 is greater than 102 .
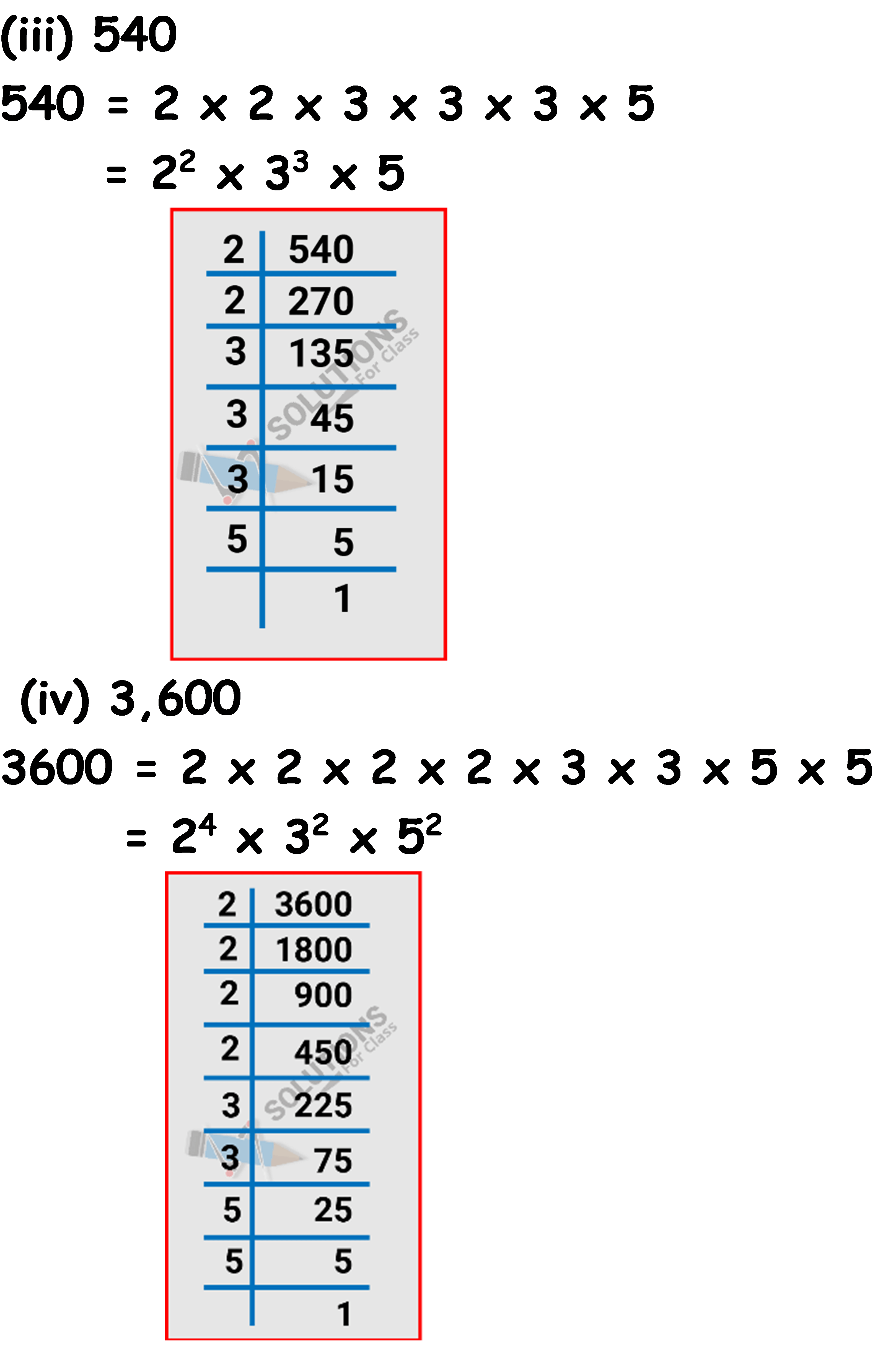
Q.5. Express each of the following as product of powers of their prime factors:
(i) 648
(ii) 405
(iii) 540
(iv) 3,600

Q.6. Simplify:
(i) 2 × 103
(ii) 72 × 22
(iii) 23 × 5
(iv) 3 × 44
(v) 0 × 102
(vi) 52 × 33
(vii) 24 × 32
(viii) 32 × 104
Ans:
(i) 2 × 103
= 2 x 10 x 10 x 10
= 2 x 1000 = 2000
(ii) 72 × 22
= 7 x 7 x 2 x 2
= 49 x 4 = 196
(iii) 23 × 5
= 2 x 2 x 2 x 5
= 8 x 5
= 40
(iv) 3 × 44
= 3 x 4 x 4 x 4 x 4
= 3 x 256
= 768
(v) 0 × 102
= 0 x 10 x 10
= 0 x 100
= 0
(vi) 52 × 33
= 5 x 5 x 3 x 3 x 3
= 25 x 27
= 675
(vii) 24 × 32
= 2 x 2 x 2 x 2 x 3 x 3
= 16 x 9
= 144
(viii) 32 × 104
= 3 x 3 x 10 x 10 x 10 x 10
= 9 x 10000
= 90000
Q.7. Simplify:
(i) (– 4)3
(ii) (–3) × (–2)3
(iii) (–3)2 × (–5)2
(iv) (–2)3 × (–10)3
Ans:
(i) (– 4)3
= (- 4) x ( – 4) x (- 4) = – 64
(ii) (–3) × (–2)3
= (- 3) x (- 2) x (- 2) x (- 2)
= (- 3) x (– 8) = 24
(iii) (–3)2 × (–5)2
= (-3) x (-3) x (-5) x (-5)
= 9 x 25 = 225
(iv) (–2)3 × (–10)3
= (- 2) x (- 2) x (- 2) x (-10) x(-10) x (-10)
= (- 8) x (–1000) = 8000
Q.8. Compare the following numbers:
(i) 2.7 × 1012; 1.5 × 108
(ii) 4 × 1014; 3 × 1017
Ans:
(i) 2.7 × 1012; 1.5 × 108
On comparing the exponents of base 10,
2.7 x 1012 > 1.5 x108
(ii) 4 × 1014; 3 × 1017
On comparing the exponents of base 10,
4×1014 < 3×1017

