
Table of Contents
ToggleClass 7, Maths, Chapter 12, Exercise 12.2 Solutions
Q.1. Simplify combining like terms:
(i) 21b – 32 + 7b – 20b
(ii) – z2 + 13z2 – 5z + 7z3 – 15z
(iii) p – (p – q) – q – (q – p)
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
(v) 5x2y – 5x2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)

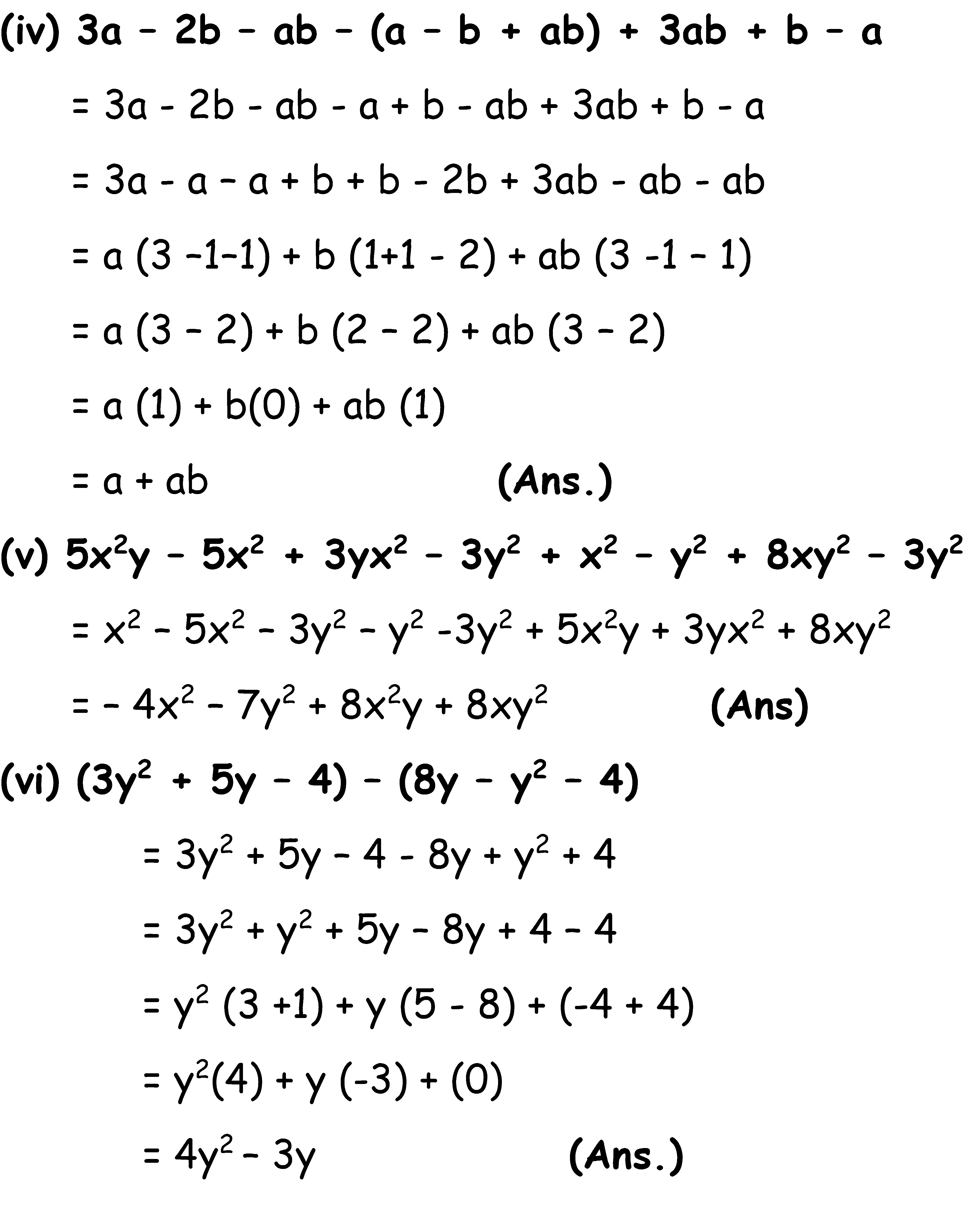
Q.2. Add:
(i) 3mn, – 5mn, 8mn, – 4mn
(ii) t – 8tz, 3tz – z, z – t
(iii) – 7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
(iv) a + b – 3, b – a + 3, a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x2y, – 3xy2, –5xy2, 5x2y
(viii) 3p2q2 – 4pq + 5, – 10 p2q2, 15 + 9pq + 7p2q2
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2










Q.3. Subtract:
(i) –5y2 from y2
(ii) 6xy from –12xy
(iii) (a – b) from (a + b)
(iv) a (b – 5) from b (5 – a)
(v) –m2 + 5mn from 4m2 – 3mn + 8
(vi) – x2 + 10x – 5 from 5x – 10
(vii) 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2
(viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
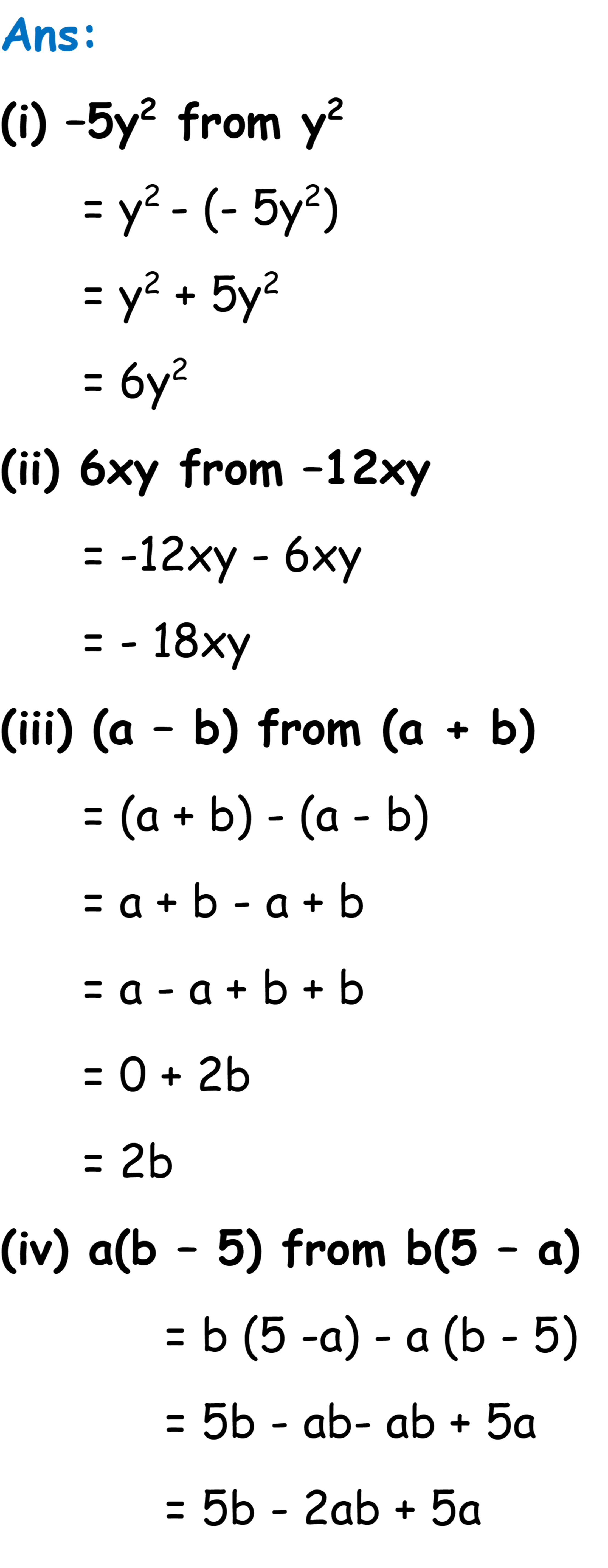




Q.4. (a) What should be added to x2+ xy + y2 to obtain 2x2 + 3xy?
(b) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
Ans:
(a) What should be added to x2+ xy + y2 to obtain 2x2 + 3xy:

(b) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16

Q.5. What should be taken away from 3x2 – 4y2 + 5xy + 20 to obtain – x2 – y2 + 6xy + 20 ?

Q.6. (a) From the sum of 3x – y + 11 and – y – 11, subtract 3x – y – 11.
(b) From the sum of 4 + 3x and 5 – 4x + 2x2, subtract the sum of 3x2 – 5x and –x2 + 2x + 5.
Ans:
(a) From the sum of 3x – y + 11 and – y – 11, subtract 3x – y – 11.

(b) From the sum of 4 + 3x and 5 – 4x + 2x2, subtract the sum of 3x2 – 5x and –x2 + 2x + 5.

NCERT Solutions For Class 7 Maths, Chapter 12 Algebraic Expressions (All Exercises)
Class 7, Maths, Chapter 12, Algebraic Expressions
Class 7, Maths, Chapter 12, Algebraic Expressions, Exercise 12.1
Class 7, Maths, Chapter 12, Algebraic Expressions, Exercise 12.2 ← You are here
Class 7, Maths, Chapter 12, Algebraic Expressions, Exercise 12.3
Class 7, Maths, Chapter 12, Algebraic Expressions, Exercise 12.4

