Table of Contents
ToggleClass 7, Maths, Chapter 1, Exercise 1.4 Solutions
Q.1. Evaluate each of the following:
(a) (–30) ÷ 10
(b) 50 ÷ (–5)
(c) (–36) ÷ (–9)
(d) (– 49) ÷ (49)
(e) 13 ÷ [(–2) + 1]
(f) 0 ÷ (–12)
(g) (–31) ÷ [(–30) + (–1)]
(h) [(–36) ÷ 12] ÷ 3
(i) [(– 6) + 5)] ÷ [(–2) + 1]
Ans:
(a) (-30) ÷ 10
= (-30) ÷ 10
= – 3
When we divide a negative integer by a positive integer, we first divide them as whole numbers and then put minus sign (-) before the quotient.
(b) 50 ÷ (-5)
= (50) ÷ (-5)
= – 10
When we divide a positive integer by a negative integer, we first divide them as whole numbers and then put minus sign (-) before the quotient.
(c) (-36) ÷ (-9)
= (-36) ÷ (-9)
= 4
When we divide a negative integer by a negative integer, we first divide them as whole numbers and then put positive sign (+) before the quotient.
(d) (- 49) ÷ (49)
= (-49) ÷ 49
= – 1
When we divide a negative integer by a positive integer, we first divide them as whole
numbers and then put minus sign (-) before the quotient.
(e) 13 ÷ [(-2) + 1]
= 13 ÷ [(-2) +1]
= 13 ÷ (-1)
= – 13
When we divide a positive integer by a negative integer, we first divide them as whole numbers and then put minus sign (-) before the quotient.
(f) 0 ÷ (-12)
= 0 ÷ (-12)
= 0
When we divide zero by a negative integer gives zero.
(g) (-31) ÷ [(-30) + (-1)]
= (-31) ÷ [(-30) + (-1)] [Use BODMASS Rule]
= (-31) ÷ [-30 – 1]
= (-31) ÷ (-31)
= 1
When we divide a negative integer by a negative integer, we first divide them as whole numbers and then put positive sign (+) before the quotient.
(h) [(-36) ÷ 12] ÷ 3
First, we have to solve the integers with in the bracket,
= [(-36) ÷ 12]
= (-36) ÷ 12
= – 3
Then,
= (-3) ÷ 3
= – 1
When we divide a negative integer by a positive integer, we first divide them as whole numbers and then put minus sign (-) before the quotient.
(i) [(- 6) + 5)] ÷ [(-2) + 1]
The given question can be written as,
= [-1] ÷ [-1]
= 1
When we divide a negative integer by a negative integer, we first divide them as whole numbers and then put positive sign (4) before the quotient.
Q.2. Verify that a ÷ (b + c) ≠ (a ÷ b) + (a ÷c) for each of the following values of a, b and c.
(a) a = 12, b = – 4, c = 2
(b) a = (–10), b = 1, c = 1


Q.3. Fill in the blanks:
(a) 369 ÷ _____ = 369
(b) (–75) ÷ _____ = –1
(c) (–206) ÷ _____ = 1
(d) – 87 ÷ _____ = 87
(e) _____ ÷ 1 = – 87
(f) _____ ÷ 48 = –1
(g) 20 ÷ _____ = –2
(h) _____ ÷ (4) = –3


Q.4. Write five pairs of integers (a, b) such that a ÷ b = –3. One such pair is (6, –2) because 6 ÷ (–2) = (–3).
Ans:
(i) (15, -5) Because, 15 ÷ (-5) = (-3)
(ii) (-15, 5) Because, (-15) ÷ (5) = (-3)
(iii) (18, -6) Because, 18 ÷ (-6) = (-3)
(iv) (-18, 6) Because, (-18) ÷ 6 = (-3)
(v) (21, -7) Because, 21 ÷ (-7) = (-3)
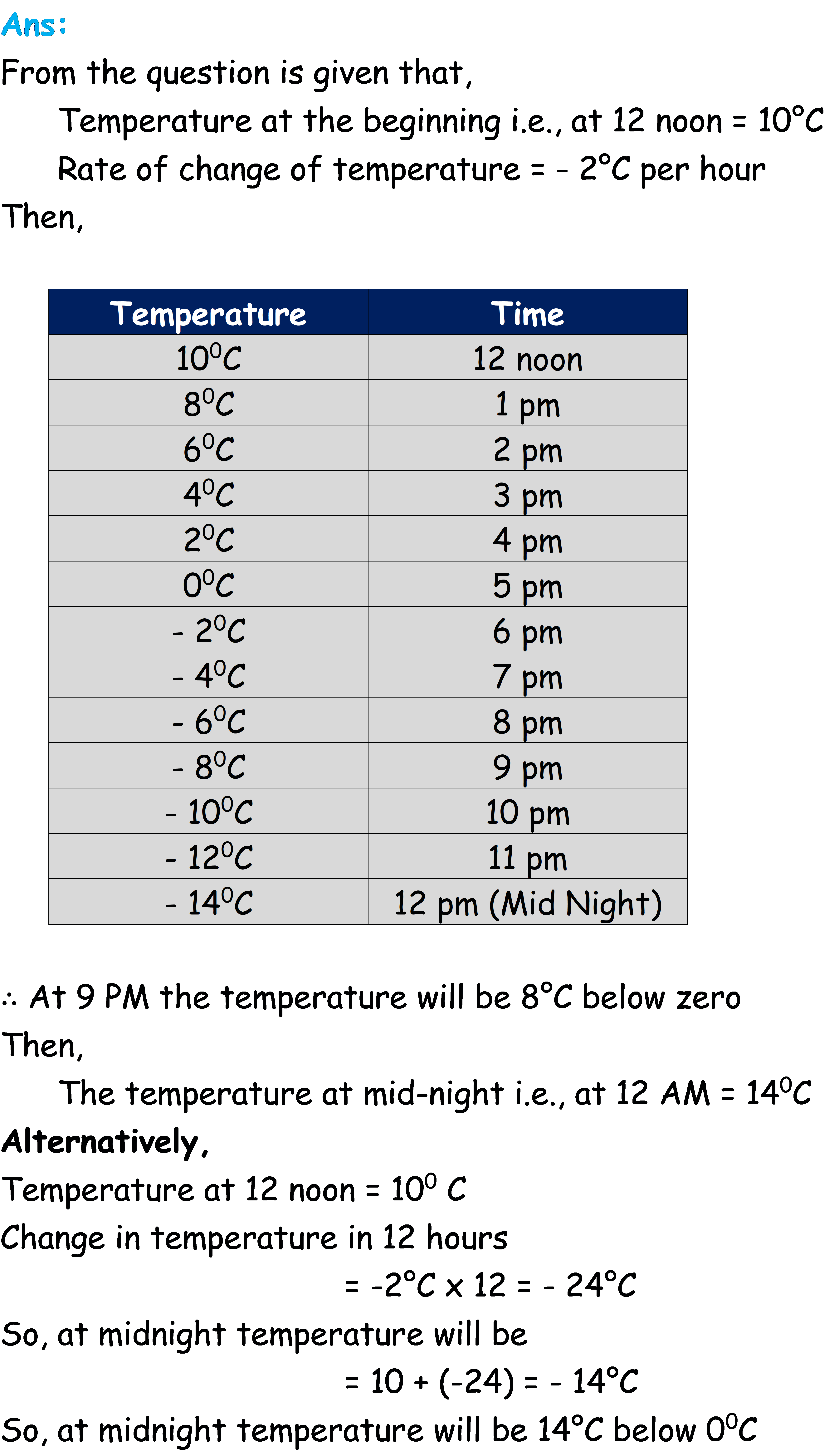
Q.5. The temperature at 12 noon was 10°C above zero. If it decreases at the rate of 2°C per hour until midnight, at what time would the temperature be 8°C below zero? What would be the temperature at mid-night?
Q.6. In a class test (+ 3) marks are given for every correct answer and (–2) marks are given for every incorrect answer and no marks for not attempting any question.
(i) Radhika scored 20 marks. If she has got 12 correct answers, how many questions has she attempted incorrectly?
(ii) Mohini scores –5 marks in this test, though she has got 7 correct answers. How many questions has she attempted incorrectly?


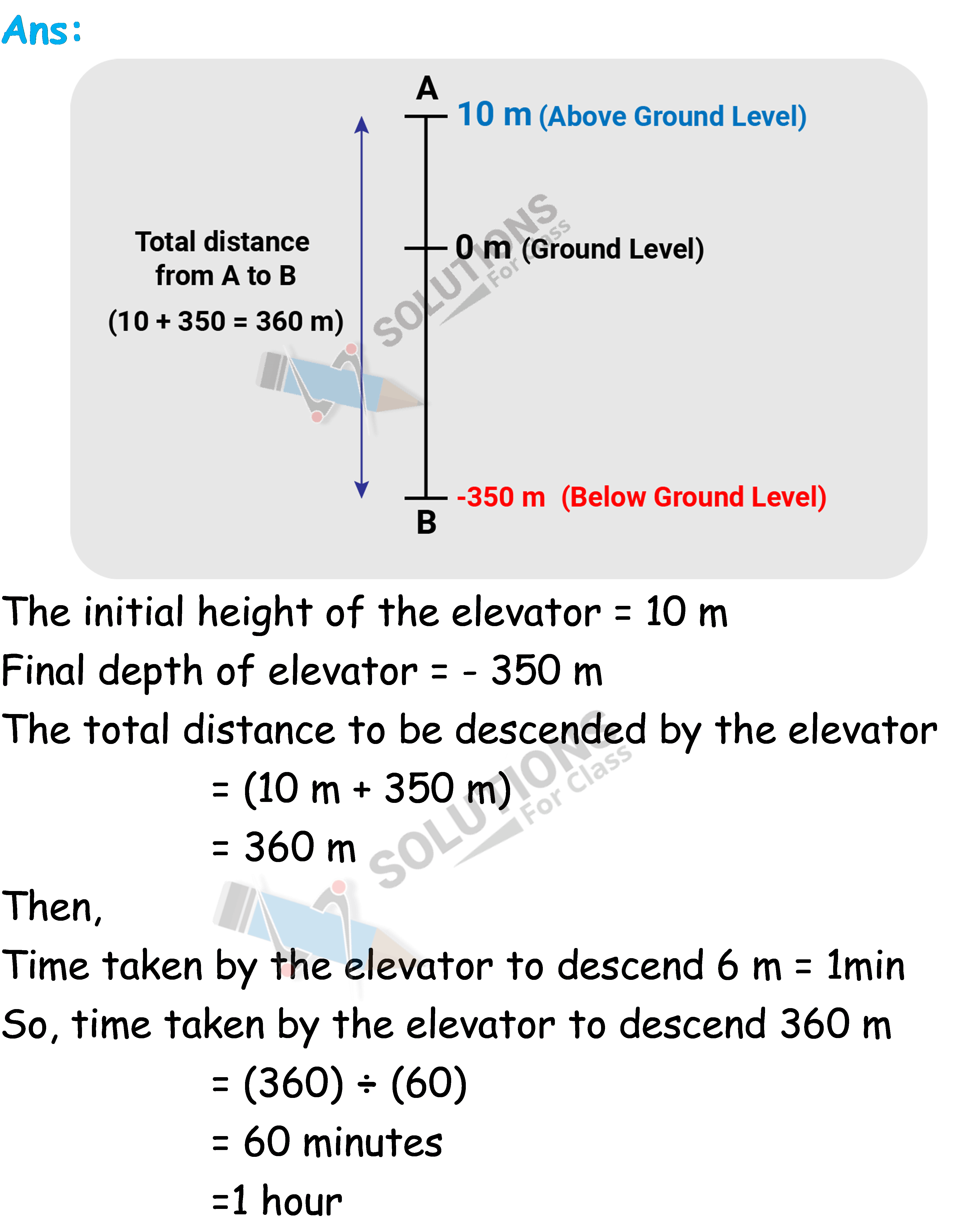
Q.7. An elevator descends into a mine shaft at the rate of 6 m/min. If the descent starts from 10 m above the ground level, how long will it take to reach – 350 m.