Class 9, Maths, Chapter 5, Exercise 5.2, Solutions
Q.1. How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
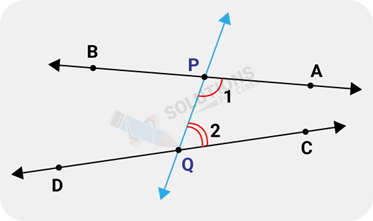
Ans: According to Euclid’s fifth postulate when the line PQ in Figure falls on lines AB and CD such that ∠1+ ∠2< 180° on the right side of PQ. then the two lines AB and CD, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
Q.2. Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Ans: If a straight-line ‘M’ falls on two straight lines ‘X’ and ‘Y’ such that the sum of the interior angles on one side of ‘M’ is two right angles, then by Euclid’s fifth postulate the lines will not meet on the left side of ‘M’.
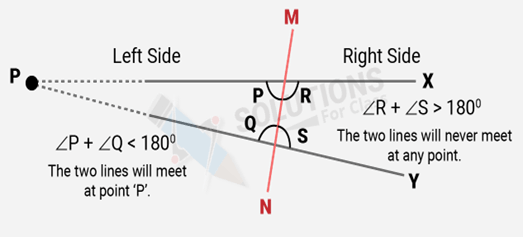
Next, we know that the sum of the interior angles on the other side of line ‘M’ will also be two right angles. Therefore, they will not meet on the other side also.
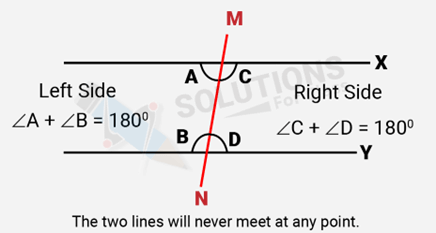
So, the lines ‘X’ and ‘Y’ never meet and are, therefore, parallel.