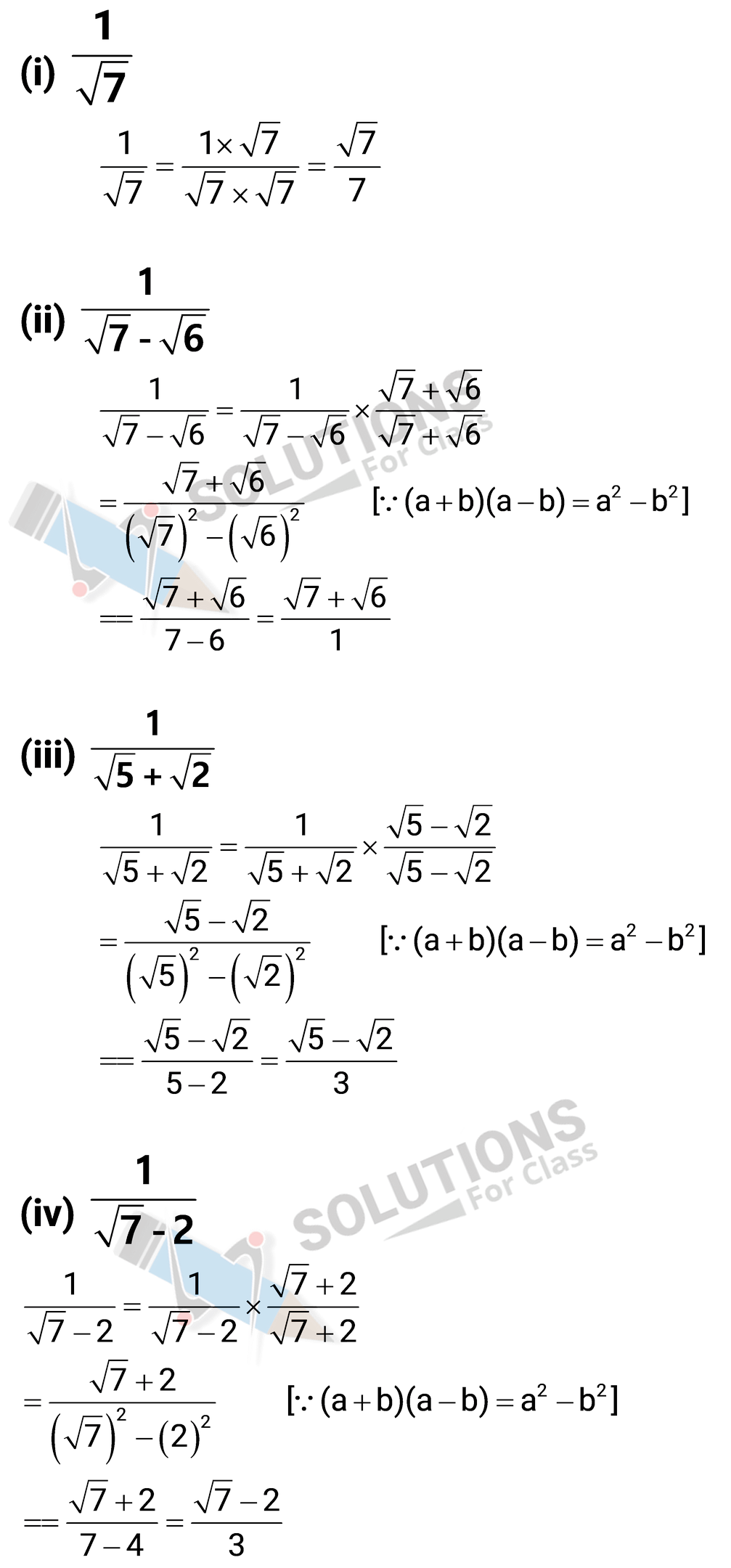Class 9 Maths Chapter 1 Exercise 1.5 Solutions
Q.1. Classify the following numbers as rational or irrational:
(i) $2-\sqrt{5}$
(ii) $\left( 3+\sqrt{23} \right)-\sqrt{23}$
(iii) $\frac{2\sqrt{7}}{7\sqrt{7}}$
(iv) $\frac{1}{\sqrt{2}}$
(v) 2𝛑
Ans:
Q.2. Simplify each of the following expressions:
(i) $\left( 3+\sqrt{3} \right)\left( 2+\sqrt{2} \right)$
(ii) $\left( 3+\sqrt{3} \right)\left( 3-\sqrt{3} \right)$
(iii) ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$
(iv) $\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)$
Ans:
Q.3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, $\pi =\frac{C}{D}$. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Ans: Writing $\pi \,\,as\,\,\frac{22}{7}$ is not the exact value. It is an approximate value and also a non – terminating, non-repeating decimal. Which means π is irrational number.
if we calculate the value of $\,\,\frac{22}{7}$, we get
$\,\,\frac{22}{7}=3.142857142857143$
∴ $\pi \,\,\ne \,\,\frac{22}{7}$
Therefore, π is an irrational number.
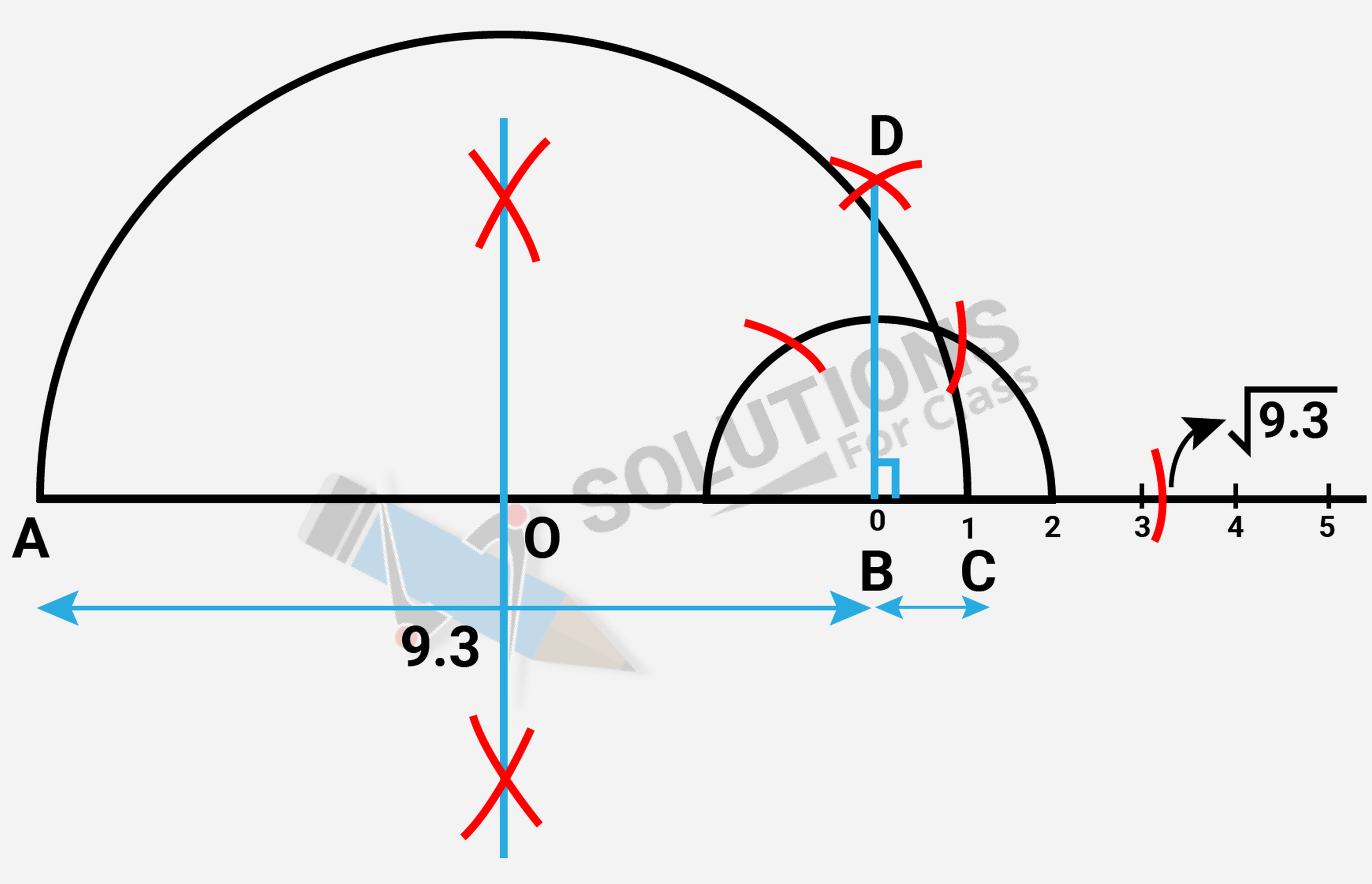
Q.4. Represent x $\sqrt{9.3}$. on the number line.
Ans:
Q.5. Rationalize the denominators of the following:
(i) $\frac{1}{\sqrt{7}}$
(ii) $\frac{1}{\sqrt{7}-\sqrt{6}}$
(iii) $\frac{1}{\sqrt{5}+\sqrt{2}}$
(iv) $\frac{1}{\sqrt{7}-2}$
Ans:
