NCERT Solution For Class 9, Maths, Chapter 13, Surface Areas And Volumes, Exercise 13.3, is the very imported exercise for students of class 9 maths. This exercise 13.3, Chapter 13, class 9 basically involves study of Curved surface area of cone and their day to day examples. Class 9, maths chapter 13, ex 13.3 solutions are given below.
Table of Contents
Toggle
Class 9, Maths, Chapter 13, Exercise 13.3 Solutions (Page no. 221)
Q.1. Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Ans: Here, r = $\frac{10.5}{2}$ = 5.25 cm and l = 10.
Curved surface area of the cone = (πrl) cm2
= $\left( \frac{22}{7}\times 5.25\times 10 \right)c{{m}^{2}}$
= 165 cm2
Q.2. Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Ans: here, $r=\frac{24}{2}=12$ cm and l = 21 m.
Total surface area of the cone = (πrl + πr2) m2
= πr (l + r) m2
= $\frac{22}{7}\times 12\times (21+12)\,{{m}^{2}}$
= $\frac{22}{7}\times 12\times 33\,{{m}^{2}}$
= 1244.57 m2 (approx.)
Q.3. Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
(i) radius of the base and (ii) total surface area of the cone.
Ans: (i) Curved surface of a cone = 308 cm2
Slant height, l = 14 cm
Let r be the radius of the base.
∴ πrl = 308
⟹ $\frac{22}{7}\times r\times 14=308$
⟹ $r=\frac{308\times 7}{22\times 14}=7$
Thus, the radius of the base = 7 cm
(ii) Total surface area of the cone = πr(l + r)
⟹ $\frac{22}{7}\times 7\times (14+7)c{{m}^{2}}$
⟹ (22×21) cm2
⟹ 462 cm2
Q.4. A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹70.
Ans:

Q.5. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use π = 3.14).
Ans:

Q.6. The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹210 per 100 m2.
Ans:
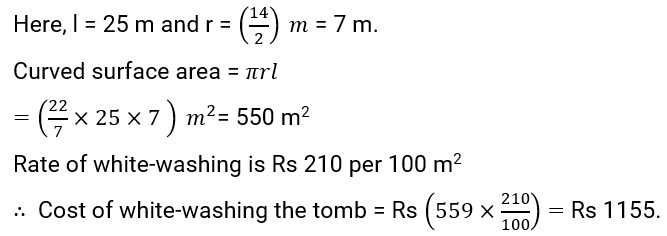
Q.7. A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Ans:

Q.8. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹12 per m2, what will be the cost of painting all these cones? (Use π = 3.14 and take$\sqrt{1.04}=1.02$
Ans:

NCERT Solutions For Class 9, Maths, Chapter 13, Surface Areas And Volumes (All Exercises)
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.1
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.2
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.3
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.4
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.5
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.6
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.7
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.8
- Class 9, Maths, Surface Areas And Volumes, Exercise 13.9

