
Table of Contents
ToggleClass 8, Maths, Chapter 9, Exercise 9.2, Solutions
Q.1. Find the product of the following pairs of monomials.
(i) 4, 7p
(ii) – 4p, 7p
(iii) – 4p, 7pq
(iv) 4p3, – 3p
(v) 4p, 0
Ans:
(i) Product of 4, 7p = 4×7P=28 P
(ii) Product of –4p,7p = (– 4p) × (7p) = -28 P2
(iii) Product of – 4p,7pq = (–4p)×(7pq) = -28 p2q
(iv) Product of 4p3,– 3p = (4p3) × (–3p) = -12p4
(v) Product of 4p, 0 = (4p) × 0 =0
Q.2. Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively. (p,q); (10m,5n); (20x2,5y2); (4x,3x2); (3mn,4np)
Ans: Area of rectangle = Length (l) X Breadth (b)
(i) (p,q)
Area of rectangle = Length (l) X Breadth (b)
= p×q
=pq square unit
(ii) (10m,5n)
Area of rectangle = Length (l) X Breadth (b)
= 10m × 5n
=50 mn square unit
(iii) (20x2, 5y2)
Area of rectangle = Length (l) X Breadth (b)
=20x2 × 5y2
= 100 x2y2 square unit
(iv) (4x,3x2)
Area of rectangle = Length (l) X Breadth (b)
= 4x × 3x2
= 12 x3 square unit
(v) (3mn,4np)
Area of rectangle = Length (l) X Breadth (b)
=3mn × 4np
= 12 mn2p squre unit
Q.3. Complete the table of products
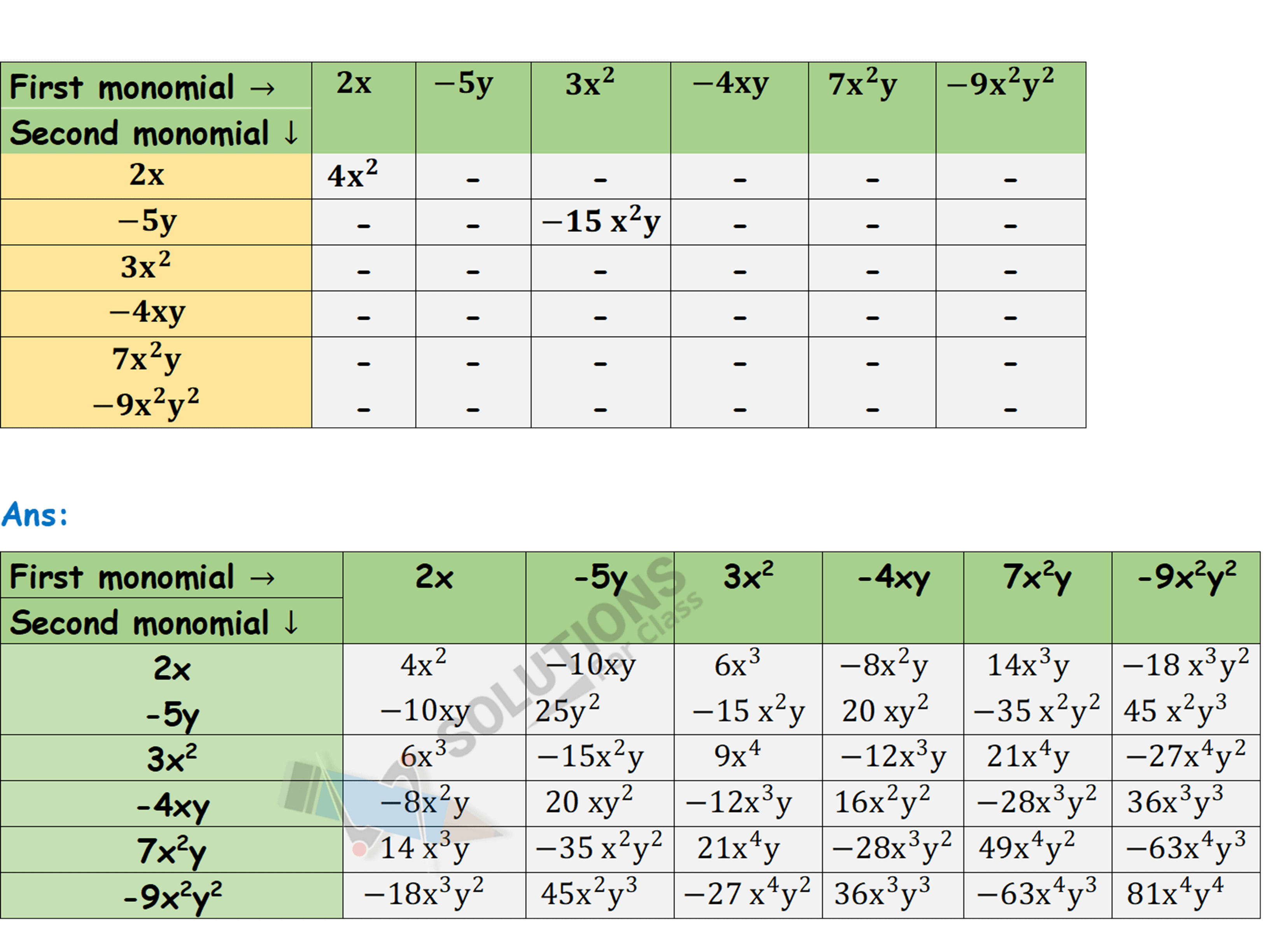
Q.4. Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
(i) 5a,3a2,7a4
(ii) 2p,4q,8r
(iii) xy,2x2y,2xy2
(iv) a,2b,3c
Ans:
Volume of rectangular box = Length x Breadth x Height
(i) 5a,3a2, 7a4
Volume of rectangular box = Length X Breadth X Height
= 5a × 3a2 × 7a4
=105 a7
(ii) 2p,4q,8r
Volume of rectangular box = Length X Breadth X Height
=2p × 4q × 8r
=64 pqr
(iii) xy,2x2y, 2xy2
Volume of rectangular box = Length X Breadth X Height
=xy × 2x2y × 2xy2
=4x4y4
(iv) a,2b,3c
Volume of rectangular box = Length X Breadth X Height
= a × 2b × 3c
=6 abc
Q.5. Obtain the product of
(i) xy,yz,zx
(ii) a,– a2, a3
(iii) 2,4y,8y2,16y3
(iv) a,2b,3c,6abc
(v) m,– mn,mnp
Ans:
(i) Product of xy,yz,zx
⇒ xy × yz × zx
⇒ x × x × y × y × z × z
⇒ x2y2z2 (Ans.)
(ii) Product of a,– a2, a3
⇒ a×(– a2) × a3
= a6 (Ans.)
(iii) Product of 2,4y,8y2, 16y3
⇒ 2 × 4y × 8y2 × 16y3
⇒ (2×4×8×16) × (y × y2 × y3)
⇒ 1024 y6 (Ans.)
(iv) Product of a,2b,3c,6abc
⇒ a × 2b × 3c × 6abc
⇒ (1 × 2 × 3 × 6) × (a × b × c × abc)
= 36 a2b2c2 (Ans.)
(v) Product of m,– mn,mnp
⇒ m×( – mn)× mnp
⇒ – m2n × mnp
⇒ -m3n2p (Ans.)
NCERT Solutions For Class 8 Maths Chapter 9, Algebraic Expressions and Identities (All Exercises)
Class 8, Maths, Chapter 9, Algebraic Expressions and Identities
Class 8, Maths, Chapter 9, Algebraic Expressions and Identities , Exercise 9.1
Class 8, Maths, Chapter 9, Algebraic Expressions and Identities , Exercise 9.2 ← You are here
Class 8, Maths, Chapter 9, Algebraic Expressions and Identities , Exercise 9.3
Class 8, Maths, Chapter 9, Algebraic Expressions and Identities , Exercise 9.4
Class 8, Maths, Chapter 9, Algebraic Expressions and Identities , Exercise 9.5

