
Table of Contents
ToggleClass 8, Maths, Chapter 10, Exercise 10.3 Solutions
Q.1. Can a polyhedron have for its faces
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Ans: (i) No, because such a polyhedron is not possible. A polyhedron has minimum 4 faces.
(ii) Yes, because a triangular pyramid has 4 triangular faces.
(iii) Yes, because a square pyramid has a square face and 4 triangular faces.
Q.2. Is it possible to have a polyhedron with any given number of faces?
Ans: yes, only if the number of faces are greater or equal to four. for example: Pyramid which has four faces.
Q. 3. Which are prisms among the following?
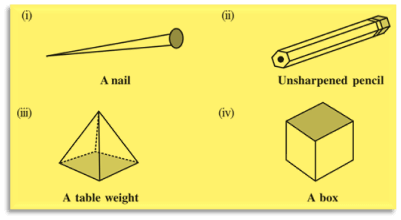
Ans:
Only (ii) unsharpened pencil and (iv) a box are the prism.
How:
(i) No, A nail cannot be a prism because there is only curved side.
(ii) Yes, An unsharped pencil is a prism because It has two identical hexagonal base and flat sides.
(iii) No, A table weight is not a prism because it doesn’t have two identical bases.
(iv) Yes, A box is a prism because It has two identical hexagonal base and flat sides.
Explanation:
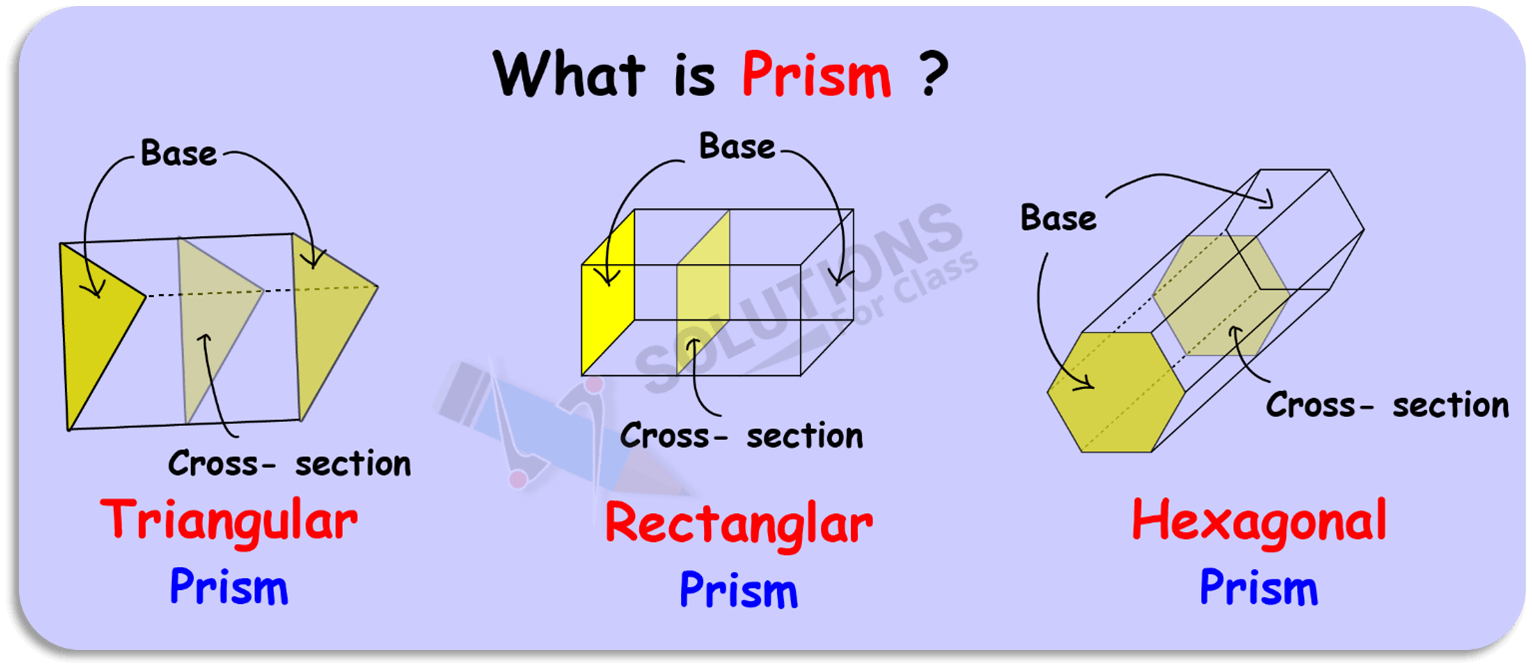
Let us know about the Prism:
Prism: it is a solid object with two faces (called the bases) that are congruent and parallel and where all cross- section are also congruent to the bases.
Q.4. (i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
Ans: (i) A prism becomes cylinder as the number of sides are increased to certain extent.
(ii) A pyramid becomes a cone as the number of sides are increased to certain extent.
Q.5. Is a square prism same as a cube? Explain.
Ans: No, a square prism and a cube are not the same.
A square prism is a shape with six rectangular faces, where three of the faces are congruent squares, and the other three faces are rectangles with the same height and width.
A cube, on the other hand, a cube is a square prism with equal length, width, and height.
So, a cube is a specific type of square prism, but not all square prisms are cubes.
Q.6. Verify Euler’s formula for these solids.
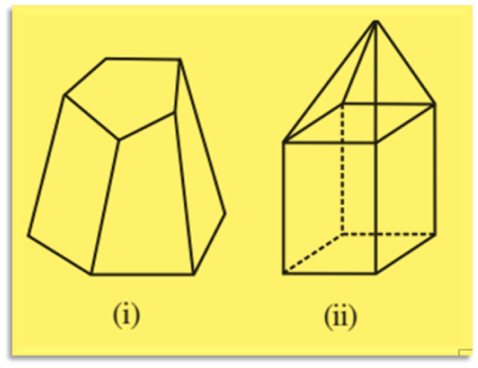
Ans: (i) Faces = 7, Sides = 15, Vertices = 10
Euler’s formula: F + V – E = 2
⇒ 7 + 10 – 15 = 2
⇒ 2 = 2
Hence, Euler’s formula is verified.
(ii) Faces = 9, Sides = 16, Vertices = 9
Euler’s Formula: F + V – E = 2
⇒ 9 + 9 – 16 = 2
⇒ 2 = 2
Hence, Euler’s formula is verified.
Q.7. Using Euler’s formula find the unknown.

Ans: Using Eulers Formula: F + V – E = 2
(i) F + 6 – 12 = 2
F – 6 = 2
F = 8
(ii) 5 + V – 9 = 2
V – 4 = 2
V = 6
(iii) 20 + 12 – E = 2
32 – E = 2
E = 30
Thus, the table can be completed as:

Q.8. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Ans: Here, Number of faces, F = 10,
Number of Edges, E = 20,
Number of Vertices, V = 15
According to Euler’s Formula:
F + V – E = 2
⇒ 10 + 15 – 20
= 25 – 20
⇒ 5 ≠ 2
Since Euler’s formula is not satisfied, such a polyhedron is not possible. Which means a polyhedron do not have 10 Faces, 20 Edges and 15 Vertices.

