
Table of Contents
ToggleClass 6, Maths, Chapter 3, Exercise 3.7 Solutions
Q.1. Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight which can measure the weight of the fertiliser exact number of times.
Ans:
Given, weight of two bags of fertiliser = 75 kg and 69 kg
For finding maximum weight, we have to find H.C.F. of 75 and 69.

Factors of 75 = 3 × 5 × 5
Factors of 69 = 3 × 23
HCF = 3
Therefore, the required weight is 3 kg.
Q.2. Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the minimum distance each should cover so that all can cover the distance in complete steps?
Ans:
First boy steps measure = 63 cm
Second boy steps measure = 70 cm
Third boy steps measure = 77 cm

For finding minimum distance, we have to find L.C.M of 63, 70 and 77
LCM = 2 × 3 × 3 × 5 × 7 × 11
= 6930
Hence, 6930 cm is the distance each should cover so that all can cover the distance in complete steps.
Q.3. The length, breadth and height of a room are 825 cm, 675 cm and 450 cm respectively. Find the longest tape which can measure the three dimensions of the room exactly.
Ans:
Given length of a room = 825 cm
Breadth of a room = 675 cm
Height of a room = 450 cm
The measurement of longest tape
= H.C.F. of 825 cm, 675 cm and 450 cm.

Factors of 825 = 3 × 5 × 5 × 11
Factors of 675 = 3 × 3 × 3 × 5 × 5
Factors of 450 = 2 × 3 × 3 × 5 × 5
HCF = 3 × 5 × 5
= 75 cm
Hence, longest tape is 75 cm which can measure the three dimensions of the room exactly.
Q.4. Determine the smallest 3-digit number which is exactly divisible by 6, 8 and 12.
Ans:
LCM of 6, 8, 12 = smallest number

LCM = 2 × 2 × 2 × 3 = 24
Smallest 3 – digit number = 100
Here, we divide 100 by 24 we get,
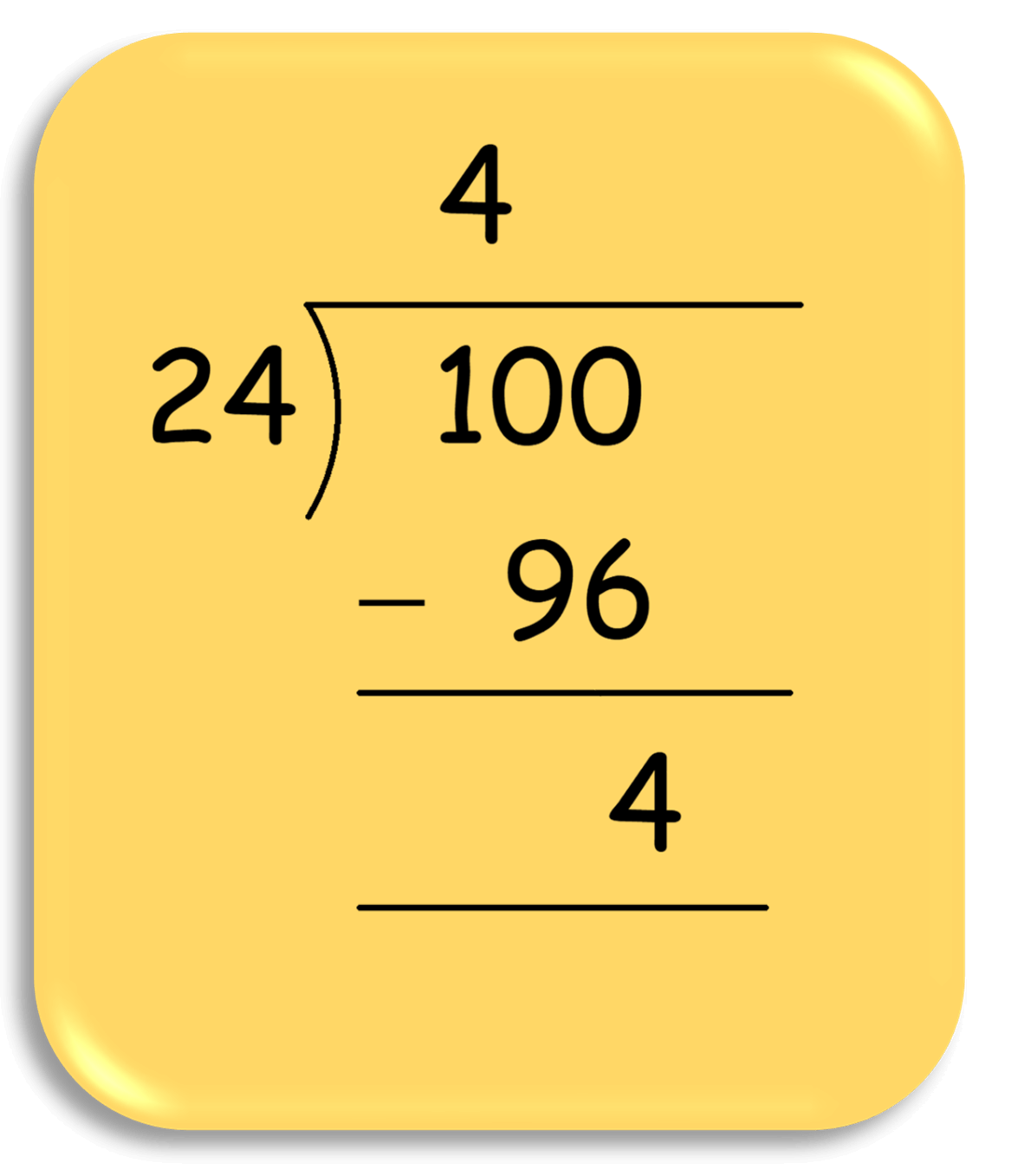
Required number is:
= 100 + (24-4)
= 100 + 20
= 120
Hence, 120 is the smallest 3-digit number which is exactly divisible by 6, 8 and 12
Q.5. Determine the greatest 3-digit number exactly divisible by 8, 10 and 12.
Ans:
LCM of 8, 10 and 12

LCM = 2 × 2 × 2 × 3 × 5 = 120
Largest 3- digit numbers = 999
Here, we divide 999 by 120. We get

Therefore, the required number:
= 999 – 39
= 960
Hence, 960 is the greatest 3-digit number exactly divisible by 8, 10 and 12
Q.6. The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m., at what time will they change simultaneously again?
Ans:
LCM of 48, 72, 108 = time period after which these lights change

LCM =
= 2 × 2 × 2 × 2 × 3 × 3 × 3
= 432
Hence, lights will change together after every 432 seconds.
432 seconds = 7 minutes 12 seconds
Therefore, the time at which they will change simultaneously again
= 7 am + 7 minutes 12 seconds
= 7 : 07 : 12 am
Q.7. Three tankers contain 403 litres, 434 litres and 465 litres of diesel respectively. Find the maximum capacity of a container that can measure the diesel of the three containers exact number of times.
Ans:
Maximum capacity of tanker required
= HCF of 403, 434, 465
Factors of 403 = 13 × 31
Factors of 434 = 2 × 7 × 31
Factors of 465 = 3 × 5 × 31
HCF = 31
Hence, a container of 31 litres is required to measure the diesel.
Q.8. Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case.
Ans:
LCM of 6, 15, 18
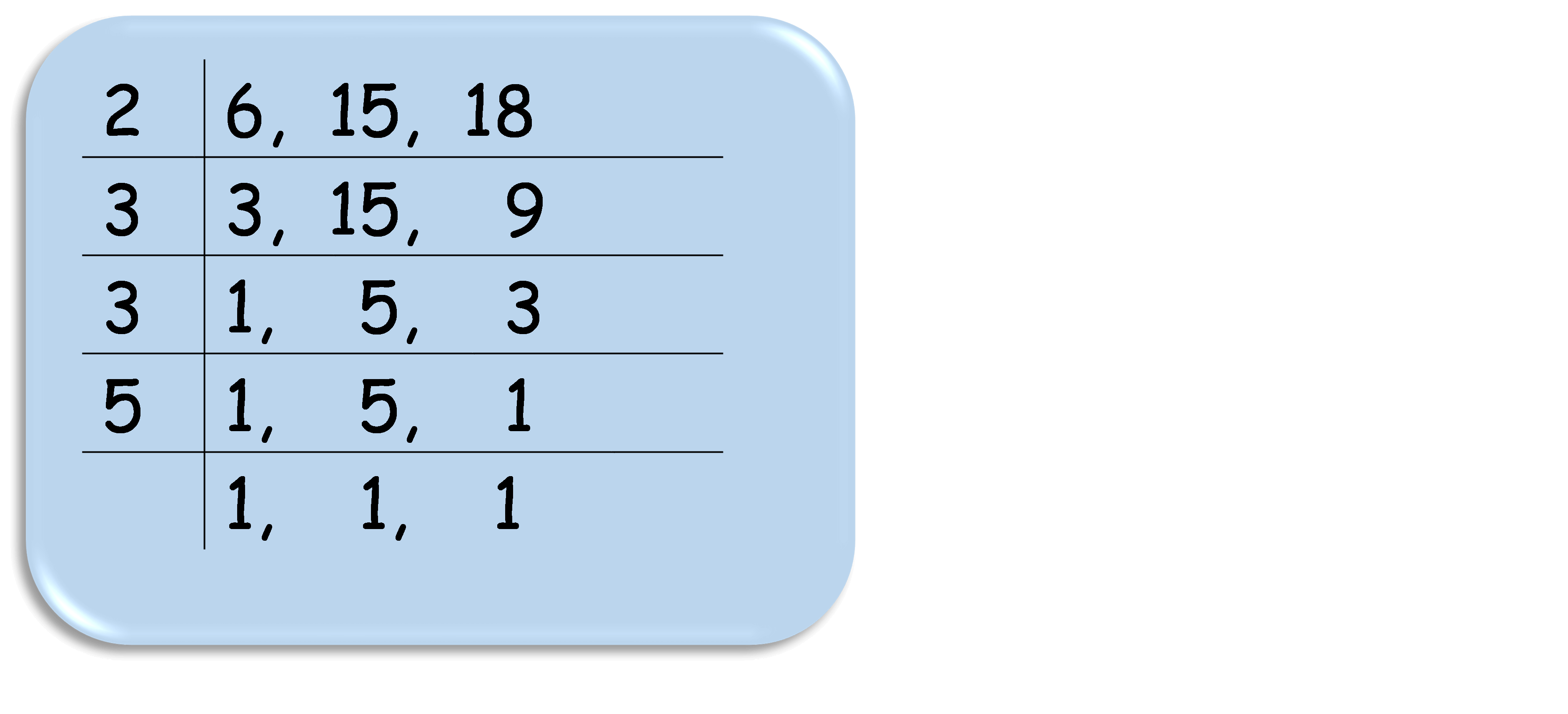
LCM = 2 × 3 × 3 × 5 = 90
Required number = 90 + 5 = 95
Hence, 95 is the required number.
Q.9. Find the smallest 4-digit number which is divisible by 18, 24 and 32.
Ans:
LCM of 18, 24, 32 :
= 2 × 2 × 2 × 2 × 2 × 3 × 3
= 288

The smallest 4-digit number is 1000.
Therefore, if divide 1000 by 288 we get,

Now, the required number:
= 1000 + (288-136)
= 1000 + 152
= 1152
Hence, 1152 is the smallest 4-digit number which is divisible by 18, 24 and 32.
Q.10. Find the LCM of the following numbers :
(a) 9 and 4
(b) 12 and 5
(c) 6 and 5
(d) 15 and 4
Observe a common property in the obtained LCMs. Is LCM the product of two numbers in each case?
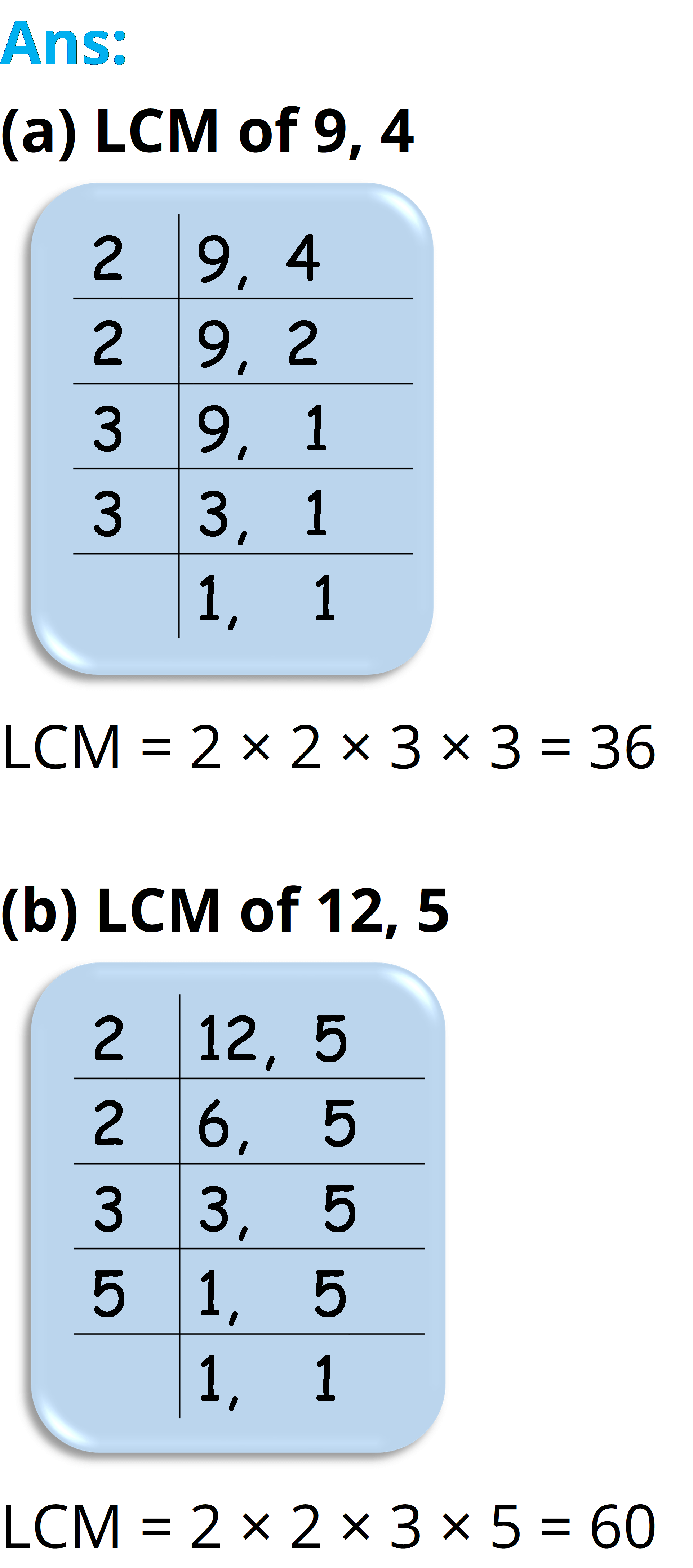
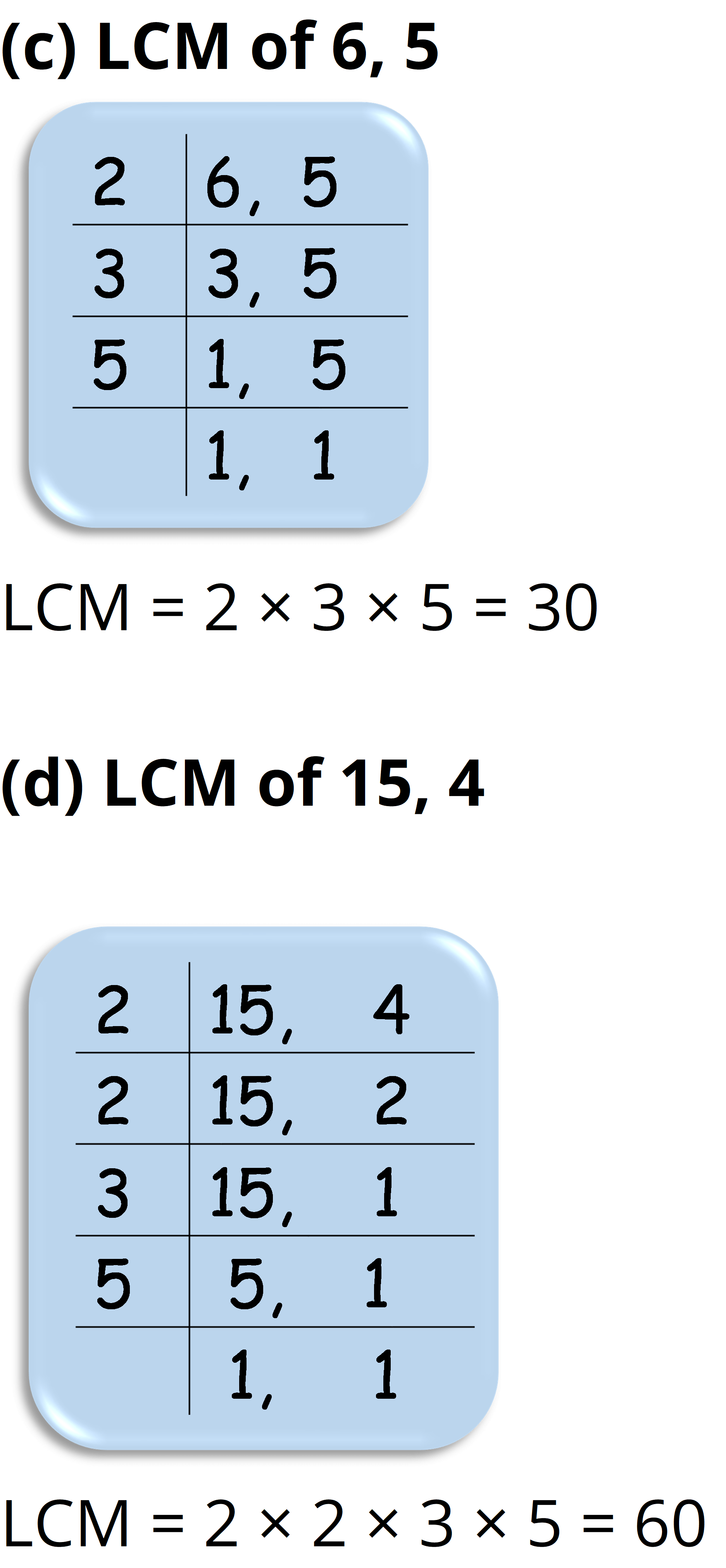
Yes, in each case the LCM of given numbers is the product of these numbers. And LCM. is also the multiple of 3
Q.11. Find the LCM of the following numbers in which one number is the factor of the other.
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45
What do you observe in the results obtained?
∴ Hence, in each case the LCM of given numbers is the larger number. When a number is a factor of other number then their LCM will be the larger number.
NCERT Solutions For Class 6 Maths, Chapter 3 Playing With Numbers (All Exercises)
Class 6, Maths, Chapter 3, Playing With Numbers
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.1
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.2
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.3
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.4
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.5
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.6
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.7 ← You are here

