
Table of Contents
ToggleNCERT Solution For Class 6, Maths, Chapter 12, Ratio And Proportion, Exercise 12.1 has total sixteen exercises to study ratio and proportions. Exercise 12.1, Chapter 12, Class 6 maths involves basically comparing ratio.
NCERT Solution For Class 6, Maths, Chapter 12, Ratio And Proportion, Exercise 12.1
Q.1. There are 20 girls and 15 boys in a class.
(a) What is the ratio of number of girls to the number of boys?
(b) What is the ratio of number of girls to the total number of students in the class?
Ans: Number of girls in a class = 20 girls
Number of boys = 15 boys
Total number of students = 20 + 15 = 35
(a) Ratio of number of girls to number of boys $=\frac{20}{15}=\frac{4}{3}=4:3$
(b) Ratio of number of girls to total number of students $=\frac{20}{35}=\frac{4}{7}=4:7$
Q.2. Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of
(a) Number of students liking football to number of students liking tennis.
(b) Number of students liking cricket to total number of students.
Ans: total number of students = 30
Number of students who like football = 6
Number of students who like cricket = 12
Number of students who like tennis = 30 –6 –12 = 12
(a) Ratio of number of students liking football that of tennis $=\frac{6}{12}=\frac{1}{2}=1:2$
(b) Ratio of number of students liking cricket to that of total students $=\frac{12}{30}=\frac{2}{5}=2:5$
Q.3. See the figure and find the ratio of

(a) Number of triangles to the number of circles inside the rectangle.
(b) Number of squares to all the figures inside the rectangle.
(c) Number of circles to all the figures inside the rectangle.
Ans: In the given figure,
Number of triangles = 3
Number of circles = 2
Number of squares = 2
Total number of figures = 7
(a) Ratio of number of triangles to that of circles $=\frac{3}{2}=3:2$
(b) Ratio of number of squares to all figures $=\frac{2}{7}=2:7$
(c) Ratio of number of circles to all figures $=\frac{2}{7}=2:7$
Q.4. Distances travelled by Hamid and Akhtar in an hour are 9 km and 12 km. Find the ratio of speed of Hamid to the speed of Akhtar.
Ans: We know that, $Speed\,\,=\frac{Distance\,(d)}{Time\,(t)} $
Distance travelled by Hamid in one hour = 9 km
∴ Speed of Hamid $=\,\,\frac{Distance\,(d)}{Time\,(t)}\,=\frac{9\,\,km}{\,hr}$
Distance travelled by Akhtar in one hour = 12 km
∴ Speed of Akhtar $=\frac{12\,\,km}{\,hr}$
Ratio of speed of Hamid to the speed of Akhtar $=\frac{9}{12}=\frac{3}{4}=3:4$
Q.5. Fill in the following blanks:
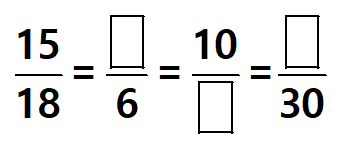
[Are these equivalent ratios?]
Ans:

Hence, 5, 12 and 25 are the numbers which come in the blanks, respectively.
Yes, these are equivalent ratios.
Q.6. Find the ratio of the following:
(a) 81 to 108
(b) 98 to 63
(c) 33 km to 121 km
(d) 30 minutes to 45 minutes
Ans: (a) 81 to 108
$=\frac{81}{108}=\frac{81\,\,\div \,9}{108\,\,\div \,\,9}=\frac{9\,\div \,3}{12\,\div \,3}=\frac{3}{4}=3:4$
Hence, the ratio of 81 to 108 = 3 : 4
(b) 98 to 63
$=\frac{98}{63}=\frac{98\,\,\div \,7}{63\,\div \,\,7}=\frac{14}{9}=14:9$
Hence, the ratio of 98 to 63 = 14 : 9
(c) 33 km to 121 km
$=\frac{33}{121}=\frac{33\,\,\div \,11}{121\,\div \,\,11}=\frac{3}{11}=3:11$
Hence, the ratio of 33 km to 121 km = 3 : 11
(d) 30 minutes to 45 minutes
$=\frac{30}{45}=\frac{30\,\,\div \,15}{45\,\div \,\,15}=\frac{2}{3}=2:\,\,3$
Hence, the ratio of 30 minutes to 45 minutes = 2 : 3
Q.7. Find the ratio of the following:
(a) 30 minutes to 1.5 hours
(b) 40 cm to 1.5 m
(c) 55 paise to ₹ 1
(d) 500 mL to 2 litres
Ans:
(a) 30 minutes to 1.5 hours
⟹ 30 minutes : 1.5 x 60 [∵ 1 hour = 60 minutes]
⟹ 30 minutes : 90 minutes
⟹ $\frac{30}{90}=\frac{3}{9}=\frac{1}{3}=1:\,\,3$
(b) 40 cm to 1.5 m
⟹ 40 cm : 1.5 x 100 cm [∵ 1 m = 100 cm]
⟹ 40 cm : 150 cm
⟹ $\frac{40}{150}=\frac{4}{15}=4:\,\,15$
(c) 55 paise to ₹ 1
⟹ 55 paise : 1 x 100 paise [∵ 1 ₹ = 100 paise]
⟹ 55 paise : 100 paise
⟹ $\frac{55}{100}=\frac{55\,\,\div \,\,5}{100\,\div \,\,5}=\frac{11}{20}=\,\,11:\,\,20$
(d) 500 mL to 2 litres
⟹ 500 ml : 2 x 1000 ml [∵ 1 Litre = 1000 ml]
⟹ 500 ml : 2000 ml
⟹ $\frac{500}{2000}=\frac{5}{20}=\frac{1}{4}=\,1:\,\,4$
Q.8. In a year, Seema earns ₹ 1,50,000 and saves ₹ 50,000. Find the ratio of
(a) Money that Seema earns to the money she saves.
(b) Money that she saves to the money she spends.
Ans: Money earned by Seema = ₹ 1,50,000
Money saved by her = ₹ 50,000
∴ Money spent by her = ₹ 1,50,000 – ₹ 50,000 = ₹ 1,00,000
(a) Ratio of money earned to money saved $=\frac{150000}{50000}=\frac{15}{5}=\frac{3}{1}=\,3:\,\,1$
(b) Ratio of money saved to money spent $=\frac{50000}{100000}=\frac{5}{10}=\frac{1}{2}=\,1:\,\,2$
Q.9. There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students.
Ans: Number of teachers = 102
Number of students = 3300
Number of teachers : Number of students
⟹ 102 : 3300
$=\frac{102}{3300}=\frac{102\,\,\div \,\,2}{3300\,\div \,\,2}=\frac{51\,\,\div \,\,3}{1650\,\div 3\,\,}=\frac{17}{550}=\,17:\,\,550$
Therefore, Ratio of number of teachers to that of students is 17:550
Q.10. In a college, out of 4320 students, 2300 are girls. Find the ratio of
(a) Number of girls to the total number of students.
(b) Number of boys to the number of girls.
(c) Number of boys to the total number of students.
Ans:
Total number of students = 4320
Number of girls = 2300
Number of boys = Total student – Number of girls
= 4320 – 2300 = 2020
(a) Number of girls to the total number of students.
$=\frac{Total\,\,number\,of\,\,Girls}{Total\,\,number\,of\,students}=\frac{2300}{4320}=\frac{230\,}{432}$ [HCF of 230 and 216 = 2]
$=\frac{230\,\div \,2}{432\div \,2}=\frac{115}{216}=\,115:\,\,216$
(b) Number of boys to the number of girls.
$=\frac{2020}{2300}=\frac{202\,\div \,2\,}{230\,\div \,2}=\frac{101}{115}=\,101:\,\,115$
(c) Number of boys to the total number of students.
$=\frac{2020}{4320}=\frac{202\,\div \,2\,}{432\,\div \,2}=\frac{101}{216}=\,101:\,\,216$
Q.11. Out of 1800 students in a school, 750 opted basketball, 800 opted cricket and remaining opted table tennis. If a student can opt only one game, find the ratio of
(a) Number of students who opted basketball to the number of students who opted table tennis.
(b) Number of students who opted cricket to the number of students opting basketball.
(c) Number of students who opted basketball to the total number of students.
Ans: Total number of students = 1800,
Number of students opted basketball = 750
Number of students opted cricket = 800
Therefore, number of students opted tennis = 1800 – (750 + 800) = 250
(a) Ratio of students opted basketball to that of opted table tennis
$=\frac{750}{250}=\frac{75\,}{25\,}=\frac{3}{1}=\,\,3:\,\,1$
(b) Ratio of students opted cricket to students opted basketball
$=\frac{800}{750}=\frac{80\,\div \,\,5}{75\,\div \,5}=\frac{16}{15}=\,\,16:\,\,15$
(c) Ratio of students opted basketball to total no. of students
$=\frac{750}{1800}=\frac{75\,\div \,\,5}{180\,\div \,5}=\frac{15\,\,\div \,3}{36\,\div \,3}=\frac{5}{12}=\,\,5:\,\,12$
Q.12. Cost of a dozen pens is ₹ 180 and cost of 8 ball pens is ₹ 56. Find the ratio of the cost of a pen to the cost of a ball pen.
Ans: Cost of a dozen pens (12 pens) = ₹ 180
∴ Cost of 1 pen $=\frac{180}{12}= $ ₹15
Cost of 8 ball pens = ₹ 56
∴ Cost of 1 ball pen $=\frac{56}{8}=$ ₹7
Ratio of cost of one pen to that of one ball pen $=\frac{15}{7}$= 15: 7
Q.13. Consider the statement: Ratio of breadth and length of a hall is 2:5. Complete the following table that shows some possible breadths and lengths of the hall.
![]()
Ans:
![]()
Q.14. Divide 20 pens between Sheela and Sangeeta in the ratio of 3:2.
Ans: Sum of ratio = 3+2 = 5
Now,
Sheela will get $=\frac{3}{5}$ of total pens and Sangeeta will get $=\frac{2}{5}$ of total pens
Number of pens Sheela got $=\frac{3}{5}\times 20=\,\,3\,\times 4=12$ pens
Number of pens Sangeeta got $=\frac{2}{5}\times 20=\,\,2\,\times 4=8\,$pens
Q.15. Mother wants to divide ₹ 36 between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya is 15 years and age of Bhoomika is 12 years, find how much Shreya and Bhoomika will get.
Ans: Age of Shreya = 15 years
Age of Bhoomika = 12 years
Ratio of the age of Shreya to that of Bhoomika $=\frac{15}{12}=\frac{5}{4}=\,5\,:\,4$
Hence, mother wants to divide ₹ 36 in the ratio of 5: 4
∴ Sum of ratio = 5 + 4 = 9
Here, Shreya will get $=\frac{5}{9}$ of Rs 36 $=\frac{5}{9}\,\,\times \,\,36= 5 \times 4 $= Rs 20
Sangeeta will get $=\frac{4}{9}$ of Rs 36 $ =\frac{4}{9}\,\,\times \,\,36=\,4\,\times 4$= Rs 16
Therefore, Shreya will get ₹ 20 and Sangeeta will get ₹ 16.
Q.16. Present age of father is 42 years and that of his son is 14 years. Find the ratio of
(a) Present age of father to the present age of son.
(b) Age of the father to the age of son, when son was 12 years old.
(c) Age of father after 10 years to the age of son after 10 years.
(d) Age of father to the age of son when father was 30 years old.
Ans: Present Age of father = 42 years
Present Age of son = 14 years
(a) Present age of father to the present age of son.
Ratio of father’s present age to that of son $=\frac{42}{14}\,\,=\,\frac{3}{1}\,\,=\,\,3\,\,:\,1\,$
(b) Age of the father to the age of son, when son was 12 years old.
The son was 12 years old 2 years ago. So, the age of father 2 years ago will be
= 42 – 2 = 40 years
Therefore, Ratio of their ages $=\frac{40}{12}\,\,=\,\frac{10}{3}\,\,=\,\,10\,\,:\,\,3\,$
(c) Age of father after 10 years to the age of son after 10 years.
Age of father after 10 years = 42 + 10 = 52 years
Age of son after 10 years = 14 + 10 = 24 years
Therefore, Ratio of their ages $=\frac{52}{24}\,\,=\,\frac{26}{12}\,=\,\frac{13}{6}\,=\,13\,:\,6\,$
(d) Age of father to the age of son when father was 30 years old.
12 years ago, age of father was 30 years . At that time age of son = 14 – 12 = 2 years
Therefore, Ratio of their ages $=\frac{30}{2}\,=\,\frac{15}{1}\,=\,\,15\,:\,1\,$
Chapter 12, Ratio And Proportion
Return to : NCERT Solutions for class 6 Maths (All Chapters)

