
Table of Contents
ToggleNCERT Solution For Class 6, Maths, Chapter 11, Algebra, Exercise 11.5
Exercise 11.5
Q.1. State which of the following are equations (with a variable). Give reason for your answer. Identify the variable from the equations with a variable.
(a) 17 = x + 7
(b) (t – 7) > 5
(c) $\frac{4}{2}=2$
(d) (7 × 3) – 19 = 8
(e) 5 × 4 – 8 = 2x
(f) x – 2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = (11 × 5) – (12 × 4)
(j) 7 = (11 × 2) + p
(k) 20 = 5y
(l) $\frac{3q}{2}<5$
(m) z + 12 > 24
(n) 20 – (10 – 5) = 3 × 5
(o) 7 – x = 5
Ans: (a) 17 = x + 7
An equation with variable x
(b) (t – 7) > 5
It is not an equation as L.H.S. is greater than R.H.S.
(c)$\frac{4}{2}=2$
It is a numerical equation with no variable.
(d) (7 × 3) – 19 = 8
It is a numerical equation with no variable.
(e) 5 × 4 – 8 = 2x
An equation with variable x.
(f) x – 2 = 0
An equation with variable x.
(g) 2m < 30 (h) 2n + 1 = 11
It is not an equation as L.H.S. is less than R.H.S.
(h) 2n + 1 = 11
An equation with variable n.
(i) 7 = (11 × 5) – (12 × 4)
It is a numerical equation with no variable.
(j) 7 = (11 × 2) + p
An equation with variable p.
(k) 20 = 5y
An equation with variable y.
(l) $\frac{3q}{2}<5$
It is not an equation as L.H.S. is less than R.H.S.
(m) z + 12 > 24
It is not an equation as L.H.S. is greater than R.H.S.
(n) 20 – (10 – 5) = 3 × 5
It is a numerical equation with no variable.
(o) 7 – x = 5
An equation with variable x.
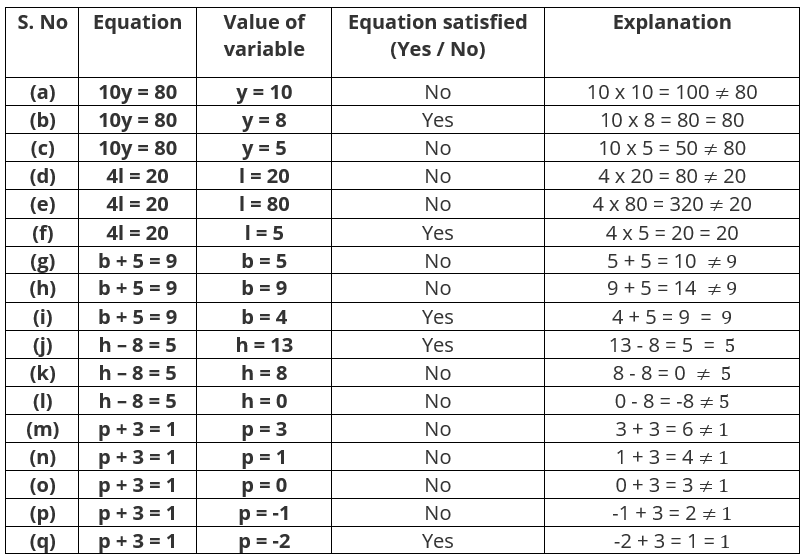
Q.2. Complete the entries in the third column of the table:

Ans:
Q.3. Pick out the solution from the values given in the bracket next to each equation. Show that the other values do not satisfy the equation.
(a) 5m = 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p – 5 = 5 (0, 10, 5 – 5)
(d) $\frac{q}{2}=7$ (7, 2, 10, 14)
(e) r – 4 = 0 (4, – 4, 8, 0)
(f) x + 4 = 2 (– 2, 0, 2, 4)
Ans: (a) 5m = 60 (10, 5, 12, 15)
Putting m = 10 5 x 10 = 50 ≠ 60 ∵ LHS ≠ RHS ∴ m =10 is not the solution | Putting m = 12 5 x 12 = 60 = 60 ∵ LHS = RHS ∴ m = 12 is the solution |
Putting m = 5 5 x 5 = 25 ≠ 60 ∵ LHS ≠ RHS ∴ m = 5 is not the solution | Putting m = 15 5 x 15 = 75 ≠ 60 ∵ LHS ≠ RHS ∴ m = 15 is not the solution |
(b) n + 12 = 20 (12, 8, 20, 0)
Putting n = 12 12 + 12 = 24 ≠ 20 ∵ LHS ≠ RHS ∴ n =12 is not the solution | Putting n = 20 20 + 12 = 32 ≠ 20 ∵ LHS ≠ RHS ∴ n =20 is not the solution |
Putting n = 8 8 + 12 = 20 = 20 ∵ LHS = RHS ∴ n =8 is the solution | Putting n = 0 0 + 12 = 12 ≠ 20 ∵ LHS ≠ RHS ∴ n =0 is not the solution |
(c) p – 5 = 5 (0, 10, 5 – 5)
Putting p = 0 0 – 5 = – 5 ≠ 5 ∵ LHS ≠ RHS ∴ p = 0 is not the solution | Putting p = 5 5 – 5 = 0 ≠ 5 ∵ LHS ≠ RHS ∴ p = 5 is not the solution |
Putting p = 10 10 – 5 = 5 ∵ LHS = RHS ∴ p = 10 is the solution | Putting p = -5 -5 – 5 = – 10 ≠ 5 ∵ LHS ≠ RHS ∴ p = -5 is not the solution |
(d) $\frac{q}{2}=7$ (7, 2, 10, 14)
Putting q = 7 $\Rightarrow \,\,\,\,\,\,\,\frac{7}{2}\,\ne \,7$ ∵ LHS ≠ RHS ∴ q = 7 is not the solution | Putting q = 10 $\Rightarrow \,\,\,\,\,\,\,\frac{10}{2}\,\ne \,7$ ∵ LHS ≠ RHS ∴ q = 10 is not the solution |
Putting q = 2 $\Rightarrow \,\,\,\,\,\,\,\frac{2}{2}\,\ne \,7$ ∵ LHS ≠ RHS ∴ q = 2 is not the solution | Putting q = 14 $\Rightarrow \,\,\,\,\,\,\,\frac{14}{2}=7=\,\,7$ ∵ LHS = RHS ∴ q = 14 is the solution |
Q.4. (a) Complete the table and by inspection of the table find the solution to the equation m + 10 = 16.
M | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | – | – | – |
M +10 | – | – | – | – | – | – | – | – | – | – | – | – | – |
Ans:
M | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
M+10 | 1+10 = 11 | 2+10= 12 | 3+10= 13 | 4+10= 14 | 5+10= 15 | 6+10= 16 | 7+10= 17 | 8+10= 18 | 9+10= 19 | 10+10= 20 | 11+10= 21 | 12+10= 22 | 13+10= 23 |
Since, for m = 6,
m + 10 = 6 + 10 = 16
∴ m is the solution.
(b) Complete the table and by inspection of the table, find the solution to the equation 5t = 35
T | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | – | – | – | – |
5t | – | – | – | – | – | – | – | – | – | – | – | – | – |
Ans:
T | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
5t | (5×3) = 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 |
At t = 7, 5t = 35
Hence, t = 7 is the solution.
(c) Complete the table and find the solution of the equation z/3 =4 using the table.
X | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | – | – | – | – |
$\frac{Z}{3}$ | $2\frac{2}{3}$ | 3 | $3\frac{1}{3}$ | – | – | – | – | – | – | – | – | – | – |
Ans:
X | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
$\frac{Z}{3}$ | $2\frac{2}{3}$ | 3 | $3\frac{1}{3}$ | $3\frac{2}{3}$ | 4 | \[4\frac{1}{3}\] | $4\frac{2}{3}$ | 5 | $5\frac{1}{3}$ | \[5\frac{2}{3}\] | 6 | $6\frac{1}{3}$ | $6\frac{2}{3}$ |
At z = 12, $\frac{Z}{3}$ = 4
Hence, z = 12 is the solution.
(d) Complete the table and find the solution to the equation m – 7 = 3
M | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | – | – | – | – |
M-7 | – | – | – | – | – | – | – | – | – | – | – | – | – |
Ans:
m | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
m – 7 | 5-7 = -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
At m = 10, m-7 = 3
Hence, m = 10 is the solution.
Q.5. Solve the following riddles, you may yourself construct such riddles.
(i) Go round a square Counting every corner Thrice and no more! Add the count to me to get exactly thirty four!
(ii) For each day of the week Make an up count from me If you make no mistake You will get twenty three!
(iii) I am a special number Take away from me a six! A whole cricket team You will still be able to fix!
(iv) Tell me who I am I shall give a pretty clue! You will get me back If you take me out of twenty two!
Ans: (i) Let I am = x,
There are 4 corners in a square.
Thrice the number of corners in the square = 3 × 4 = 12
Now, if 12 is added to the number ‘x’, it becomes 34
X + 12 = 34
X = 34 – 12 = 22
So, the number will be 22.
(ii) Let I am = x
We know that there are 7 days in a week.
∴ up counting from x for 7, the sum = 23
We have, x + 7 = 23
x = 23 – 7
X = 16
Thus, I am 16.
(iii) Let I am = x,
There are 11 players in cricket team. “Take away from me a six”, means we have to subtract 6 from x.
∴ x – 6 = 11
We get
x = 11 + 6
∴ x = 17
Thus, I am 17.
(iv) Let I am = x,
You will get me back If you take me out of twenty two.
∴ 22 – x = x
22 = 2x
$x=\frac{22}{2}=11$
∴ x = 11
Thus, i am 11.

