NCERT Solution For Class 6 Maths Chapter 11 Algebra Exercise 11.1
Exercise 11.1
Q.1. Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
(a) A pattern of letter T as T
(b) A pattern of letter Z as Z
(c) A pattern of letter U as U
(d) A pattern of letter V as V
(e) A pattern of letter E as E
(f) A pattern of letter S as S
(g) A pattern of letter A as A
Ans:
(a) A pattern of letter T as
No. of letter T = 1
No. of match sticks required = 2
Hence, the pattern is 2n.
(b) A pattern of letter Z as
No. of letter Z = 1
No. of match sticks required = 3
Hence, the pattern is 3n.
(c) A pattern of letter U as
No. of letter U = 1
No. of match sticks required = 3
Hence, the pattern is 3n.
(d) A pattern of letter V as
No. of letter V = 1
No. of match sticks required = 2
Hence, the pattern is 2n.
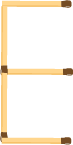
(e) A pattern of letter E as
No. of letter E = 1
No. of match sticks required = 4
Hence, the pattern is 4n.
(f) A pattern of letter S as
No. of letter S = 1
No. of match sticks required = 5
Hence, the pattern is 5n.
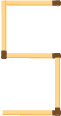
(g) A pattern of letter A as
No. of letter A = 1
No. of match sticks required = 3
Hence, the pattern is 3n.
Q.2. We already know the rule for the pattern of letters L, C and F. Some of the letters from Q.1 (given above) give us the same rule as that given by L. Which are these? Why does this happen?
Ans: We know that T require only two matchsticks. So, the pattern for letter T is 2n. Among all the letters given in question 1, only T and V are the letters which require two matchsticks. Hence, (a) and (d).
Q.3. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule which gives the number of cadets, given the number of rows? (Use n for the number of rows.)
Ans: Number of rows = n
Cadets in each row = 5
Therefore, total number of cadets = 5n
Q.4. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use b for the number of boxes.)
Ans: Let ‘b’ be the number of boxes
Number of mangoes in a box = 50
Total number of mangoes = Number of mangoes in 1 box × number of boxes
= 50 x b = 50b
Q.5. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (Use s for the number of students.)
Ans: Let s be the number of students
Pencils given to each student = 5
Total number of pencils = Number of pencils given to one student × number of students
= 5 x s = 5s
Q.6. A bird flies 1 kilometre in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes? (Use t for flying time in minutes.)
Ans: Let t minutes be the flying times
Distance covered in one minute = 1 km
Distance covered in t minutes = Distance covered in 1 minute × Flying time
= 1 × t = t km
Q.7. Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots) with chalk powder. She has 9 dots in a row. How many dots will her Rangoli have for r rows? How many dots are there if there are 8 rows? If there are 10 rows?
Ans: Number of dots in a row = 9
Number of rows = r
Total number of dots in r rows = Number of dots in a row × number of rows
= 9 x r = 9r
When there are 8 rows, then the number of dots = 8 x r = 8 × 9 = 72 dots
Number of dots in 10 rows = 9 x r = 9 × 10 = 90 dots
Q.8. Leela is Radha’s younger sister. Leela is 4 years younger than Radha. Can you write Leela’s age in terms of Radha’s age? Take Radha’s age to be x years.
Ans: Let Radha’s age = x years
Leela’s age = 4 years younger than Radha = (x – 4) years
Q.9. Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is l, how many laddus did she make?
Ans: Number of laddus gave away = /
Number of laddus remaining = 5
Total number of laddus = No. of laddus given away + No. of laddus remaining
= (l + 5) laddus
Q.10. Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?
Ans: Number of oranges in 1 small box = x
Number of boxes = 2
∴ Number of oranges in 2 small boxes = 2x
Number of oranges remained = 10
Number of oranges in large box = No. of oranges in 2 small boxes + No. of oranges remained
= 2x + 10
Q.11. (a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks
in terms of the number of squares. (Hint : If you remove the vertical stick at the end, you will get a pattern of Cs.)
(b) The given figure gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
Ans: (a) We observe that in the given matchstick pattern, the number of matchsticks are 4, 7, 10 and 13, which is 1 more than the thrice of the number of squares.
Therefore, the pattern is 3x + 1, where x is the number of squares.
Simply , No. of match sticks = 3x +1 ( where, x = no. of squares)
(b) We observe that in the given matchstick pattern, the number of matchsticks are 3, 5, 7 and 9 which is 1 more than the twice of the number of triangles in the pattern.
Therefore, the pattern is 2x + 1, where x is the number of triangles.
Simply, No. of match sticks = 2x +1 (where, x = no. of triangles)