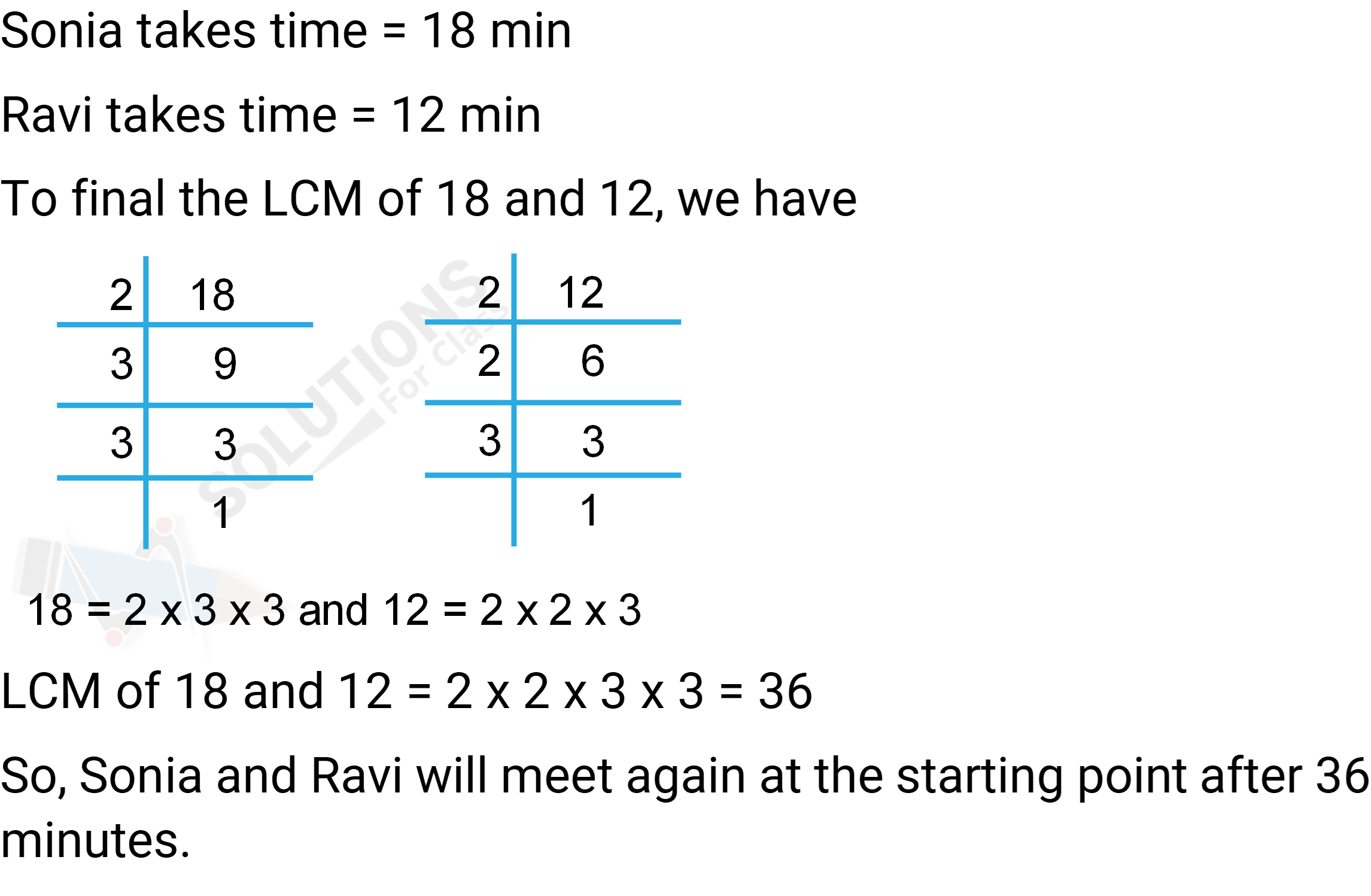NCERT Solution For Class 10, Maths, Real Numbers, Exercise 1.2 is very important for examination purpose. In this exercise we will learn how to factorization of inters and how to find HCF and LCM of a number.
Table of Contents
Toggle
Class 10, Maths, Chapter 1, Exercise 1.2, Solutions
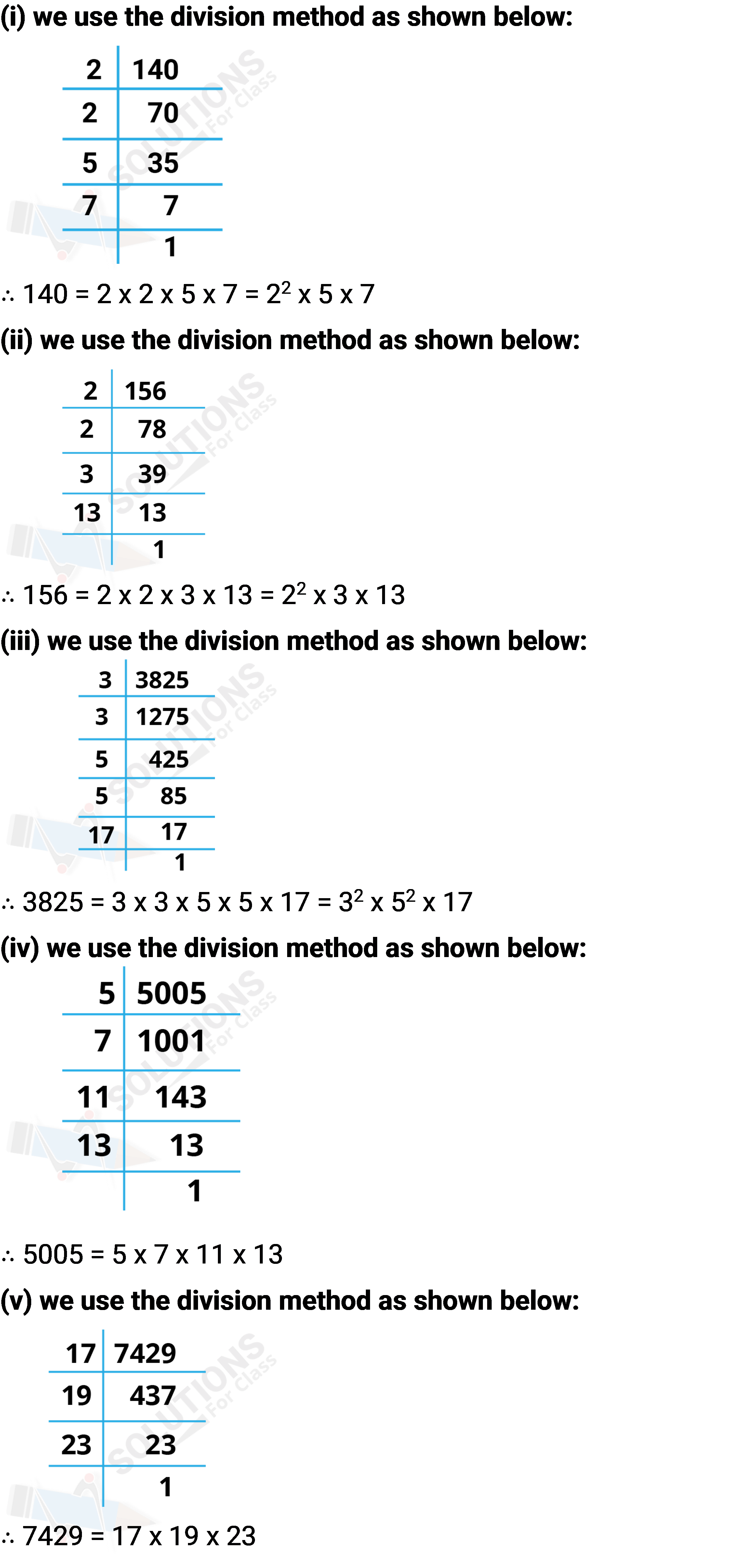
Q.1. Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Ans:
Q.2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Ans:

Q.3. Find the LCM and HCF of the following integers by applying the prime factorization method.
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Ans:

Q.4. Given that HCF (306, 657) = 9, find LCM (306, 657).
Ans:

Q.5. Check whether 6n can end with the digit 0 for any natural number n.
Ans: If the number 6n, ends with the digit zero, then it is divisible by 5. That is, a number ends with zero prime factors must be (2 x 5).
(6)n= (2 x 3)n
6n can not end with digit zero because its prime factors do not contain pair of 2 x 5.
Q.6. Explain why 7×11×13+13 and 7×6×5×4×3×2×1+5 are composite numbers.
Ans:
(i) Since, 7 × 11 × 13 + 13
⟹ 13 (7 x 11 + 1)
⟹ 13 (77 + 1)
⟹ 13 (78)
⟹ 13 (2 x 3 x 13)
The given expression has 2,3 and 13 are its factors. So, the given number is composite as they have many factors other than 1.
(ii) Since, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
⟹ 5 (7 x 6 x 4 x 3 x 2 x 1 + 1)
⟹ 5(1008 + 1)
⟹ 5 (1009) or
⟹ 5 (1009 x 1)
The given expression has 5,1009 and 1 are its factors. So, the given number is composite as they have many factors other than 1.
Q.7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Ans: