Class 10, Maths, Chapter 4, Exercise 4.2 Solutions
Q.1. Find the roots of the following quadratic equations by factorization:
(i) x2 – 3x – 10 = 0
(ii) 2x2 + x – 6 = 0
(iii) $\sqrt{2}\,{{x}^{2}}+7x+5\sqrt{2}=0$
(iv) $2{{x}^{2}}-x+\frac{1}{8}=0$
(v) 100 x2 – 20x + 1 = 0
Ans:
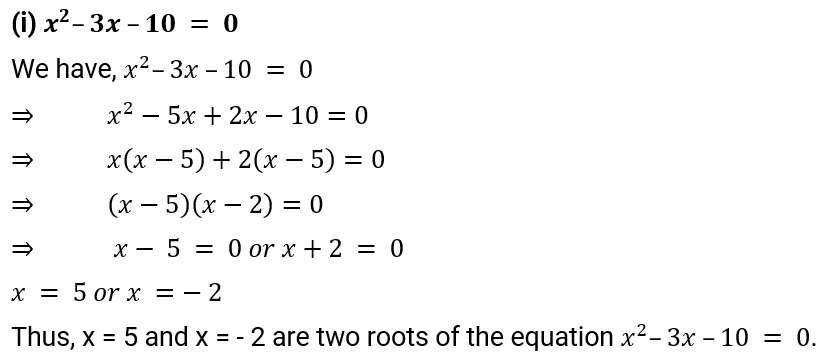
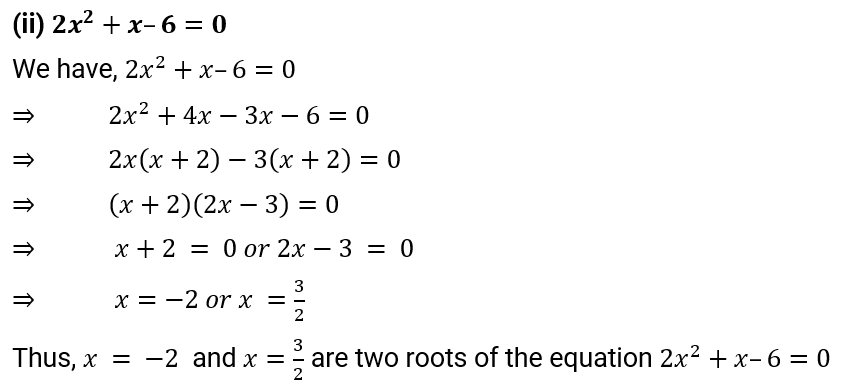
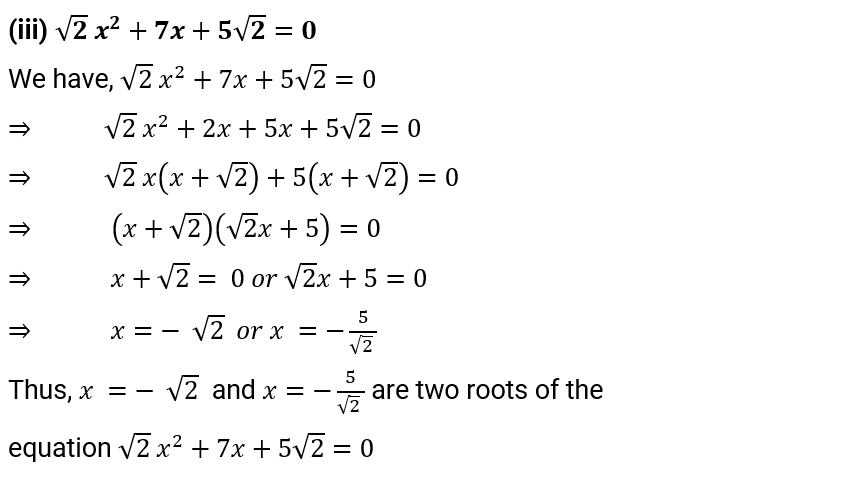
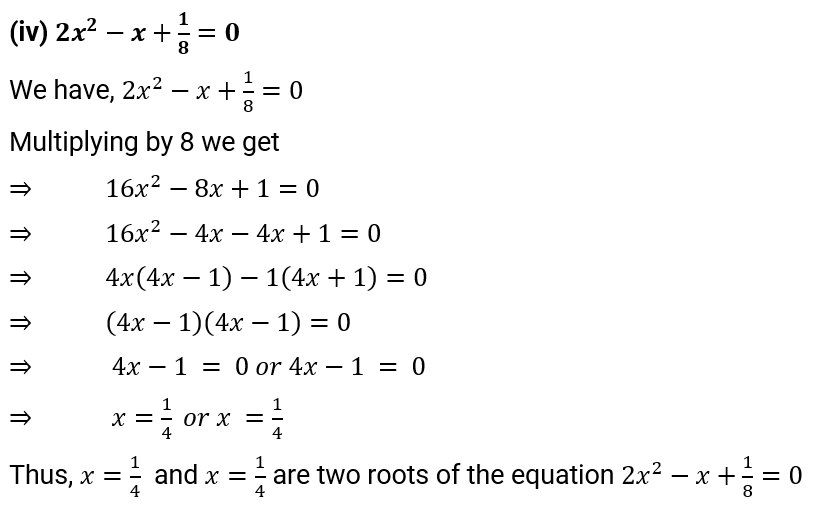
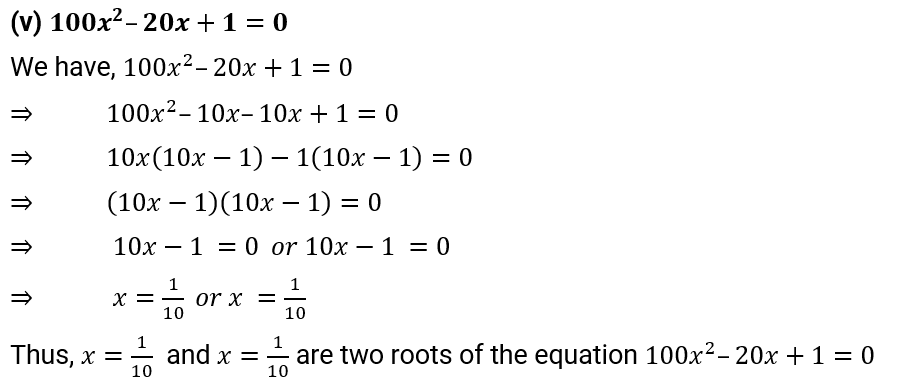
Q.2. Solve the problems given in Example 1.
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. We would like to find out the number of toys produced on that day
Ans:
(i) Let the number of marbles John had be x.
Then the number of marbles Jivanti had = 45 –x
When john lost 5 marbles, then number of marble left =x – 5
Therefore, the number of marbles left with Jivanti, when she lost 5 marbles =45 – x – 5 = 40–x
Therefore, their product =(x–5) (40–x)
= 40x–x2 – 200 + 5x
= –x2 + 45x – 200
Given the product of the number of marbles =124
So, –x2 + 45x – 200 = 124
i.e., –x2 + 45x – 324 = 0
i.e., x2 –45x + 324 = 0
Therefore, the number of marbles John had, satisfies the quadratic equation
⇒ x2–45x + 324 = 0
We have, x2 – 45x + 324 = 0
⇒ x2–9x – 36x + 324 = 0
⇒ x(x-9) – 36(x-9) = 0
⇒ (x-9) (x-36) = 0
⇒ x-9 = 0 or x – 36 =0
⇒ x = 9 or x = 36
Thus, x=9 and x=36 are two roots of the equation x2–45x + 324 = 0 or we can say that, John and Jivanti had 9 and 36 or 36 and 9 respectively.
(ii) Let the number of toys produced on that day be x.
Therefore, the cost of production (in ₹) of each toy that day = 55 – x
So, the total cost of production (in ₹) that day =x(55–x)
Therefore, x(55–x =750
i.e., 55x–x2=750
i.e., –x2 + 55x–750 =0
i.e., x2– 55x + 750 =0
Therefore, the number of toys produced that day satisfies the quadratic equation
⇒ x2–55x + 750 = 0
We have, x2–55x + 750 = 0
⇒ x2–30x – 25x + 750 = 0
⇒ x(x- 30) – 25(x-30)=0
⇒ (x-30) (x-25) = 0
⇒ x – 30 = 0 or x–25 =0
⇒ x = 30 or x =25
Thus, x=30 and x = 25 are two roots of the equation x2–55x + 750 = 0 or
We can say that
If the number of toys produced on that day be 30.
Then, the cost of production (in ₹) of each toy that day would be =55 –x=55-30=25 ₹
Or
If the number of toys produced on that day be 25.
Then, the cost of production (in ₹) of each toy that day would be =55 –x=55-25=35 ₹
Q.3. Find two numbers whose sum is 27 and product is 182.
Ans:
Q.4. Find two consecutive positive integers, sum of whose squares is 365.
Ans:
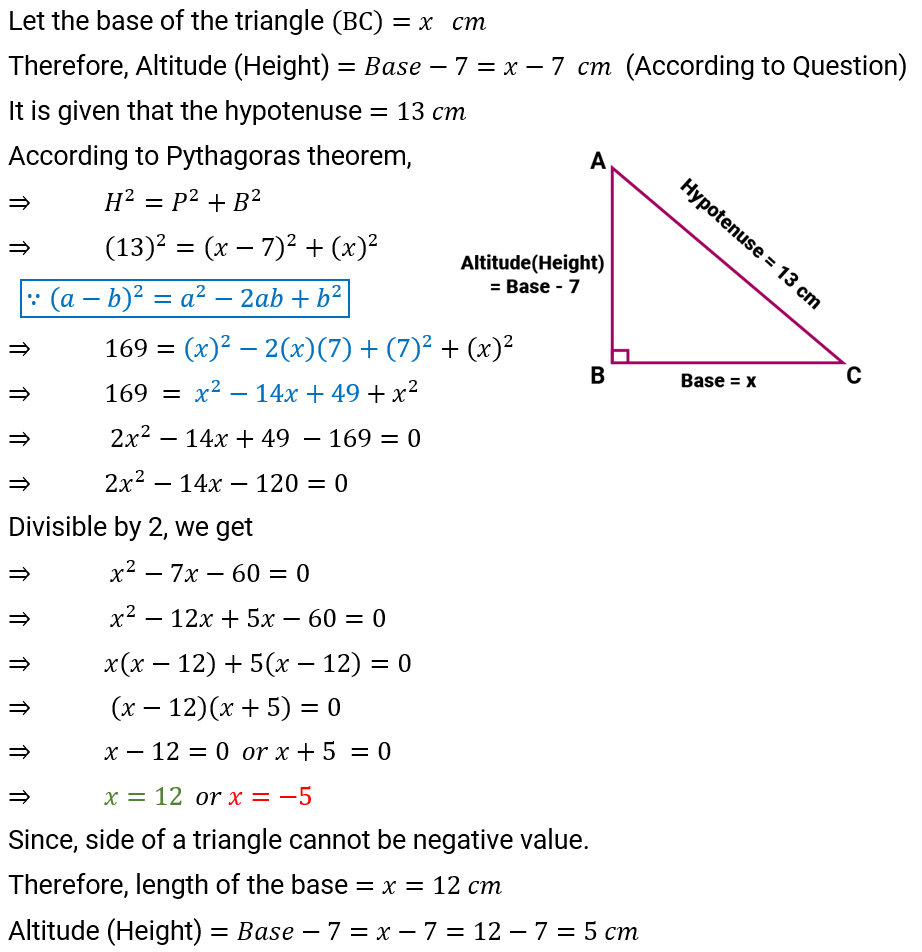
Q.5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Ans:
Q.6. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was ₹ 90, find the number of articles produced and the cost of each article.
Ans: Let the number of articles produced in a day = x
Then, cost of production of each article = ₹ (2x + 3) (according to question)
Total cost of production of each article on that day = ₹ 90
Therefore,
i.e., x(2x + 3) = 90
i.e., 2x2 + 3x = 90
i.e., 2x2 + 3x – 90 = 0
Therefore, the number of pottery articles produced that day satisfies the quadratic equation
⇒ 2x2 + 3x – 90 = 0
We have, 2x2 + 3x – 90 = 0
⇒ 2x2 – 12x + 15x – 90 = 0
⇒ 2x(x – 6) + 15(x – 6) = 0
⇒ (x – 6) (2x + 15) = 0
⇒ x – 6 = 0 or 2x + 15 = 0
⇒ x = 6 or x = $-\frac{15}{2}$
Since, the number of articles produced cannot be a negative number. Now, we can say that
If the number of articles produced on that day = x = 6
Then, the cost of production (in ₹) of each article that day would be =(2x + 3) = (2×6 + 3) = ₹ 15