NCERT Solution For Class 10, Maths, Pair Of Linear Equations In Two Variables, Exercise 3.2 includes questions related to day to day examples. Students also needs to find Which of the pairs of linear equations are consistent/inconsistent. If consistent, need to obtain the solution graphically. Class 10, Maths, chapter 3, Exercise 3.2 have total seven questions to discuses.
Table of Contents
Toggle
Class 10, Maths, Chapter 3, Exercise 3.2, Solutions
Q.1. Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Ans: (i) let us denote the number of girls by ‘x’ and the number of boys by ‘y’.
then, the equations formed are
x + y = 10 eq.(i)
And, x = y + 4
⇒ x – y = 4 eq.(ii)
Let us draw the graphs of equations (i) and (ii) by finding two solutions for each of these equations.
From eq. (i), x + y = 10
When x = 5, y = 5;
when x = 3, y = 7;
Thus, we have the following table:

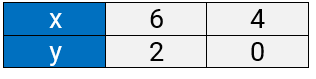
From eq. (ii), x – y = 4
When x = 6, y = 2;
when x = 4, y = 0;
Thus, we have the following table:
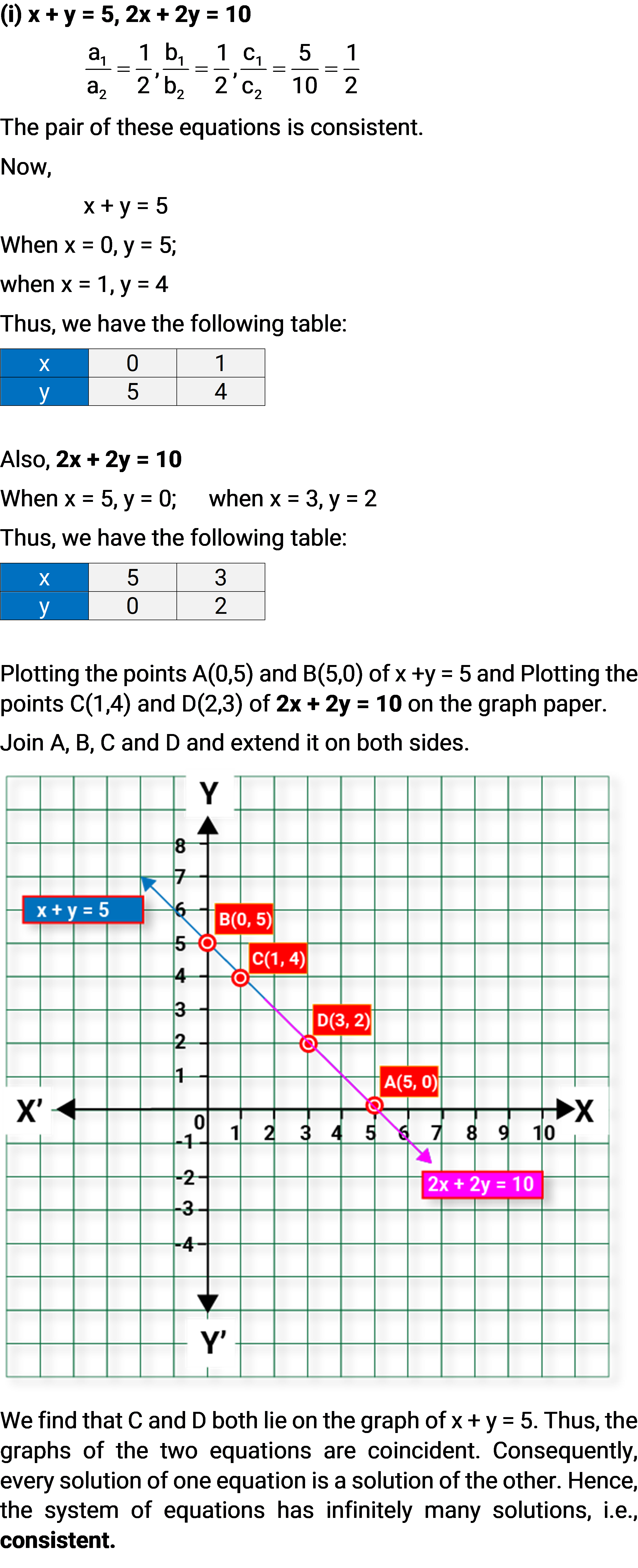
Plotting the graph from above tables, we get
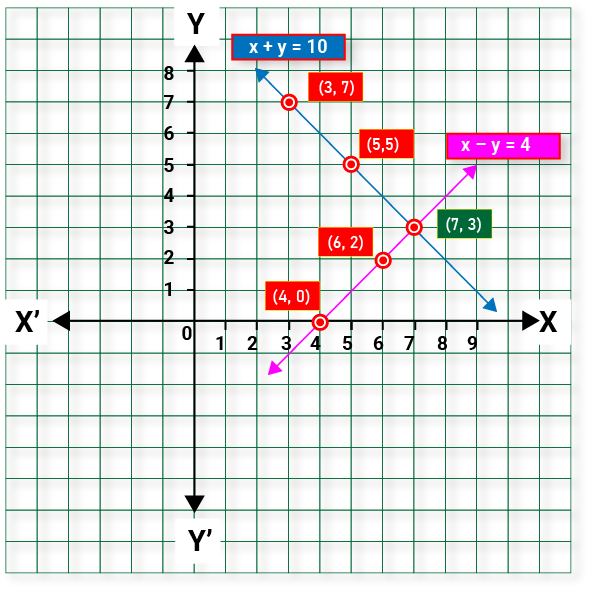
These two lines intersect at (7,3). So, x = 7 and y = 3 is the required solution.
Hence, the number of girls and boys are 7 and 3 respectively.
Verification: Put x = 7 and y = 3 in (i) and (ii), we find that both the equations are satisfied.
(ii) Let us denote the cost of one pencil by Rs x and one pen by Rs y. Then, the equations formed are
5x + 7y = 50 eq.(i)
And, 7x + 5y = 46 eq.(ii)
Let us draw the graphs of equations (1) and (2) by finding two solutions for each of these equations. The solutions of the equations are given in table.
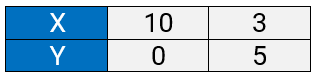
5x + 7y = 50
When x = 10, y = 0;
when x = 3, y = 5;
Thus, we have the following table:
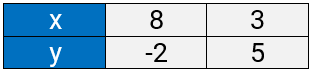
7x + 5y = 46
When x = 8, y = -2;
when x = 3, y = 5;
Thus, we have the following table:
Plotting the graph from above tables, we get
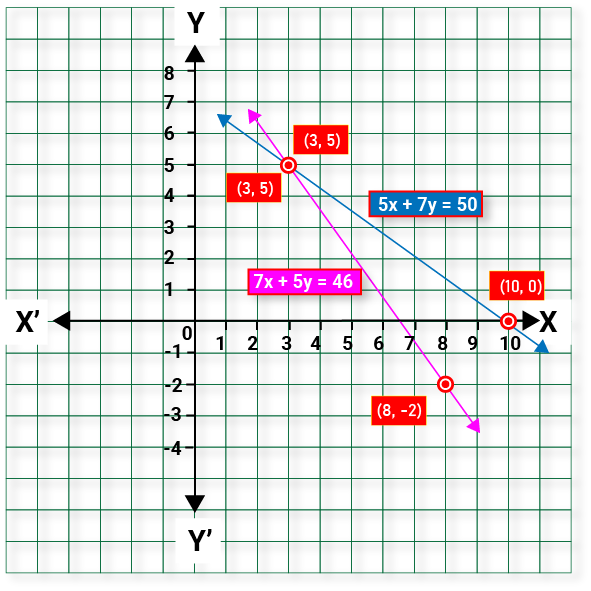
These two lines intersect at (3, 5). So, x = 3 and y = 5 is the required solution.
Hence, the cost of one pencil is Rs 3 and that of one pen is Rs 5.
Verification: Put x = 3 and y = 5 in (i) and (ii), wo find that both the equations are satisfied.
Q.2. On comparing the ratios $\frac{{{a}_{1}}}{{{a}_{2}}},\frac{{{b}_{1}}}{{{b}_{2}}}$and $\frac{{{c}_{1}}}{{{c}_{2}}}$ find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0; 2x – y + 9 = 0
Ans:


Q.3. On comparing the ratios $\frac{{{a}_{1}}}{{{a}_{2}}},\frac{{{b}_{1}}}{{{b}_{2}}}$and $\frac{{{c}_{1}}}{{{c}_{2}}}$, find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2x – 3y = 8; 4x – 6y = 9
(iii) $\frac{3}{2}x+\frac{5}{3}y=7$; 9x – 10y =14
(iv) 5x – 3y = 11; – 10x + 6y = –22
(v) $\frac{4}{3}$x + 2y = 8; 2x + 3y =12
Ans:
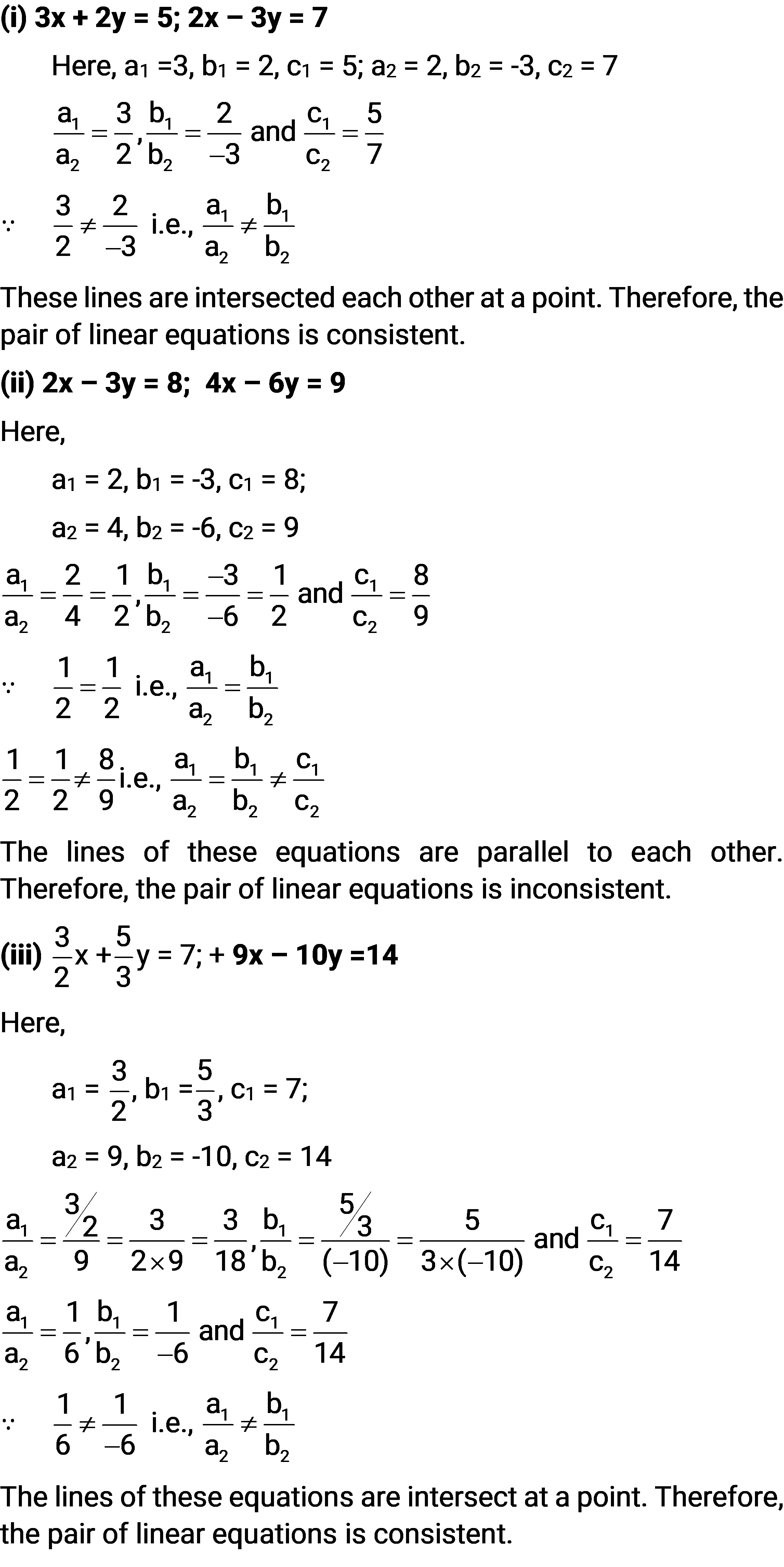
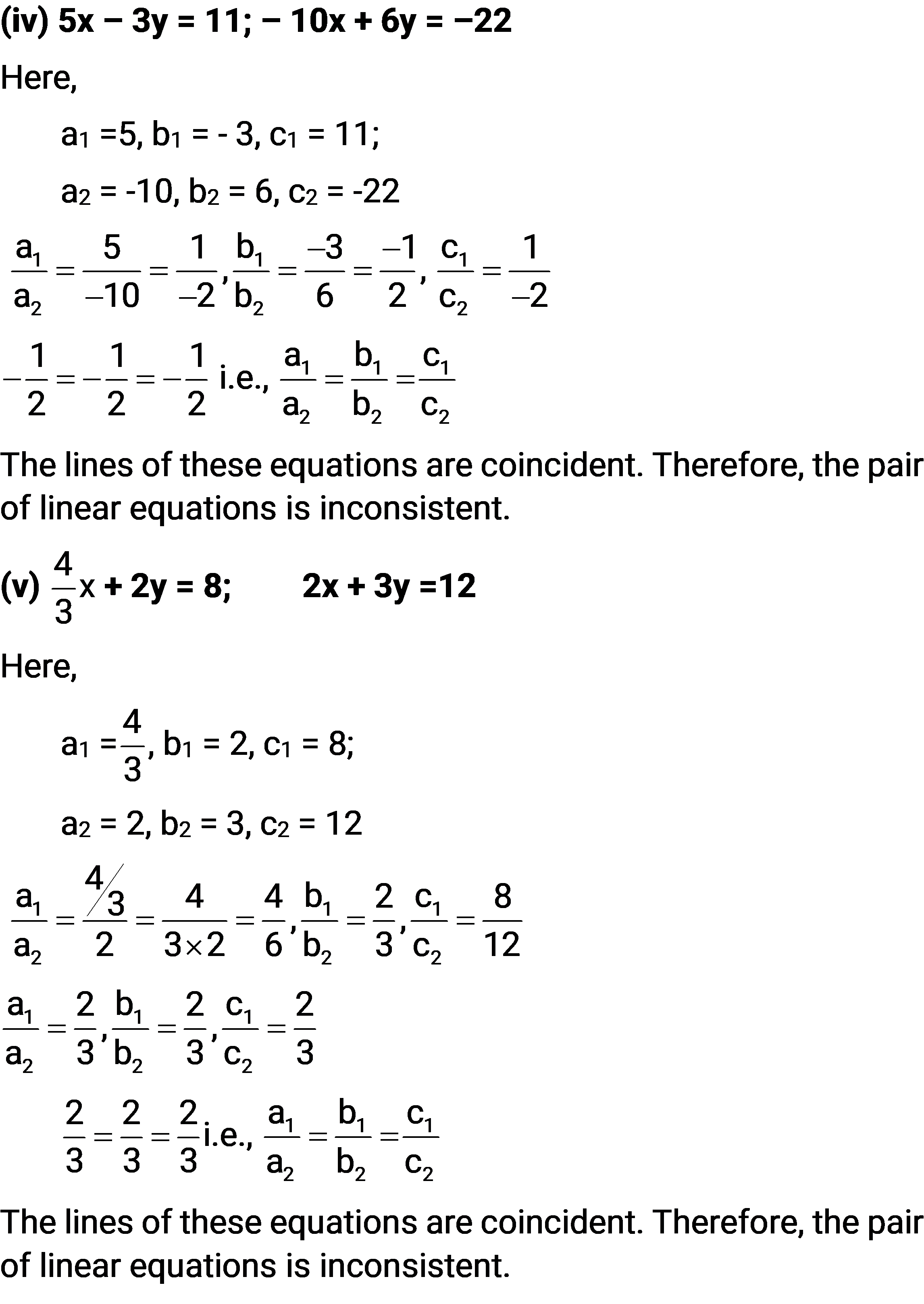
Q.4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
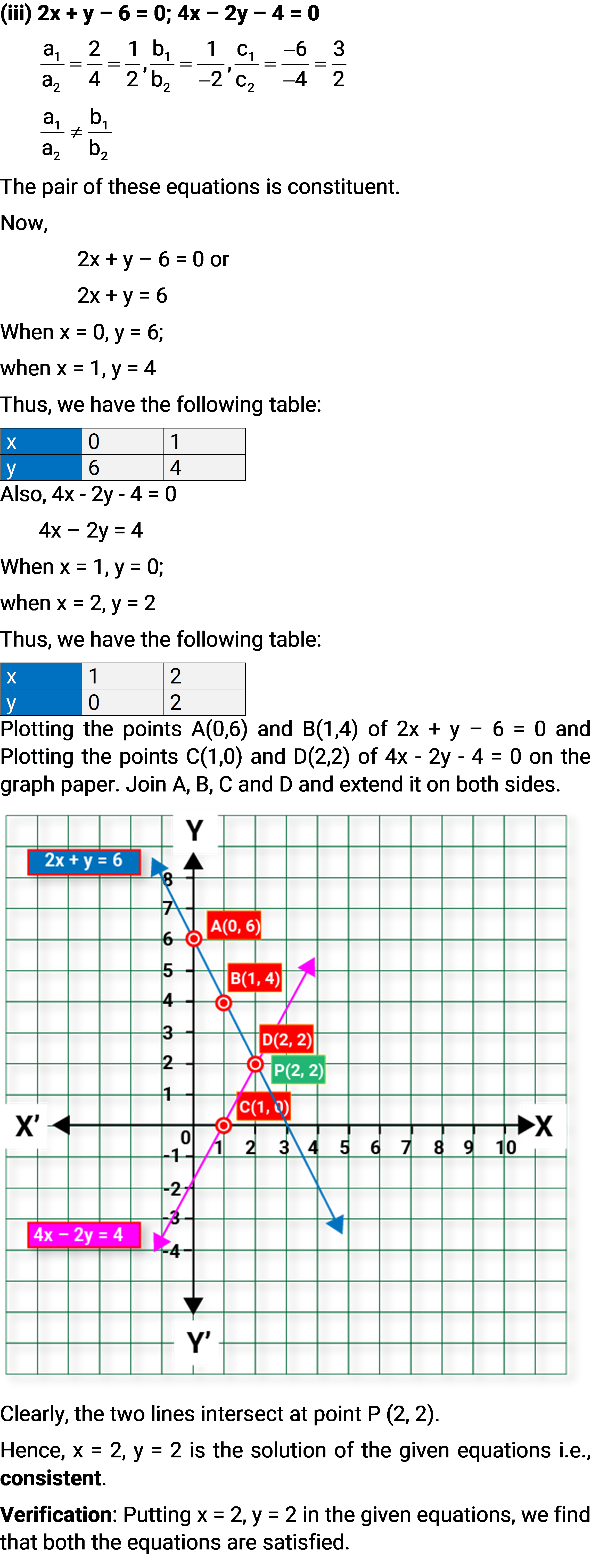
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Ans:

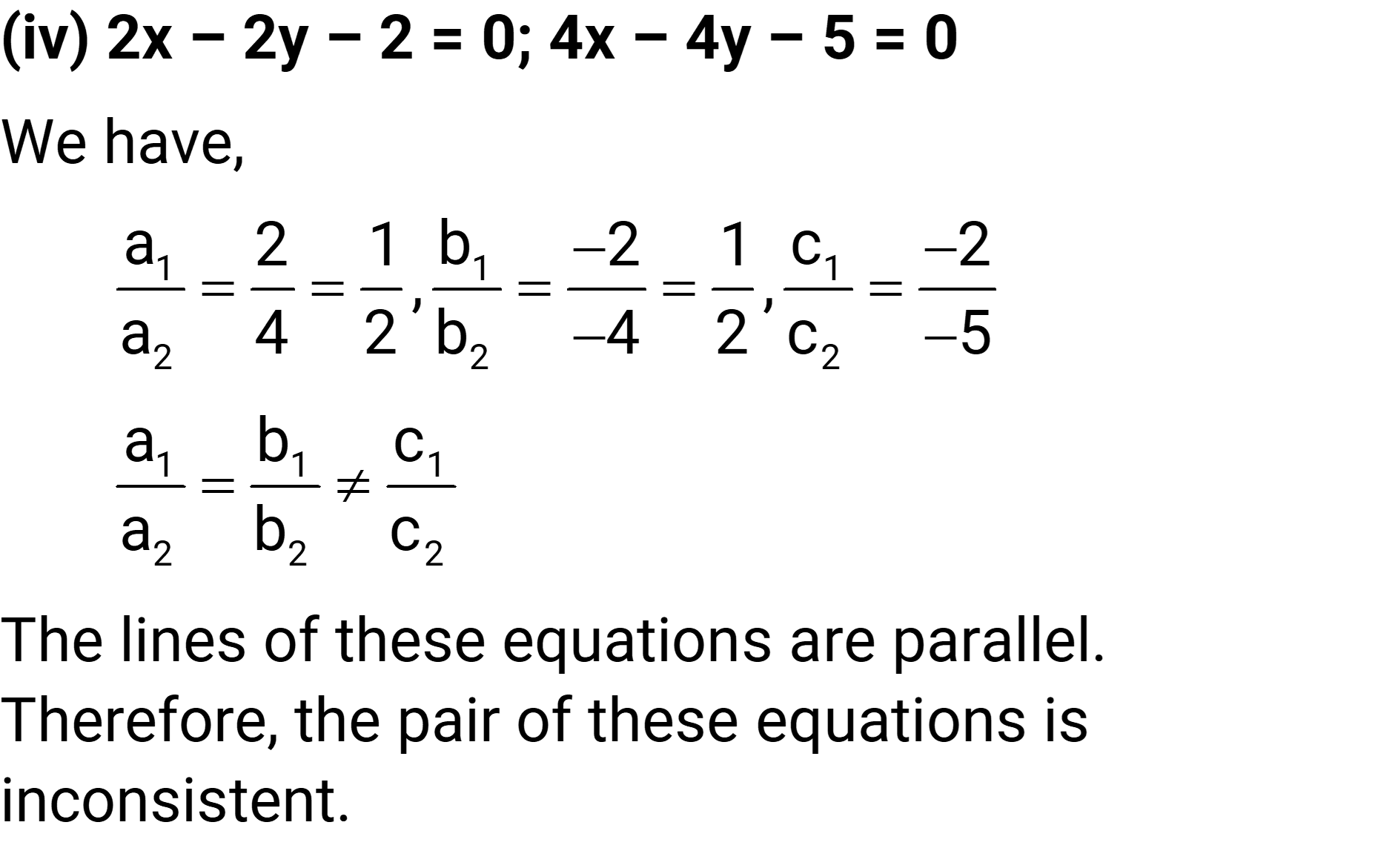
Q.5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Ans:

Q.6. Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Ans:
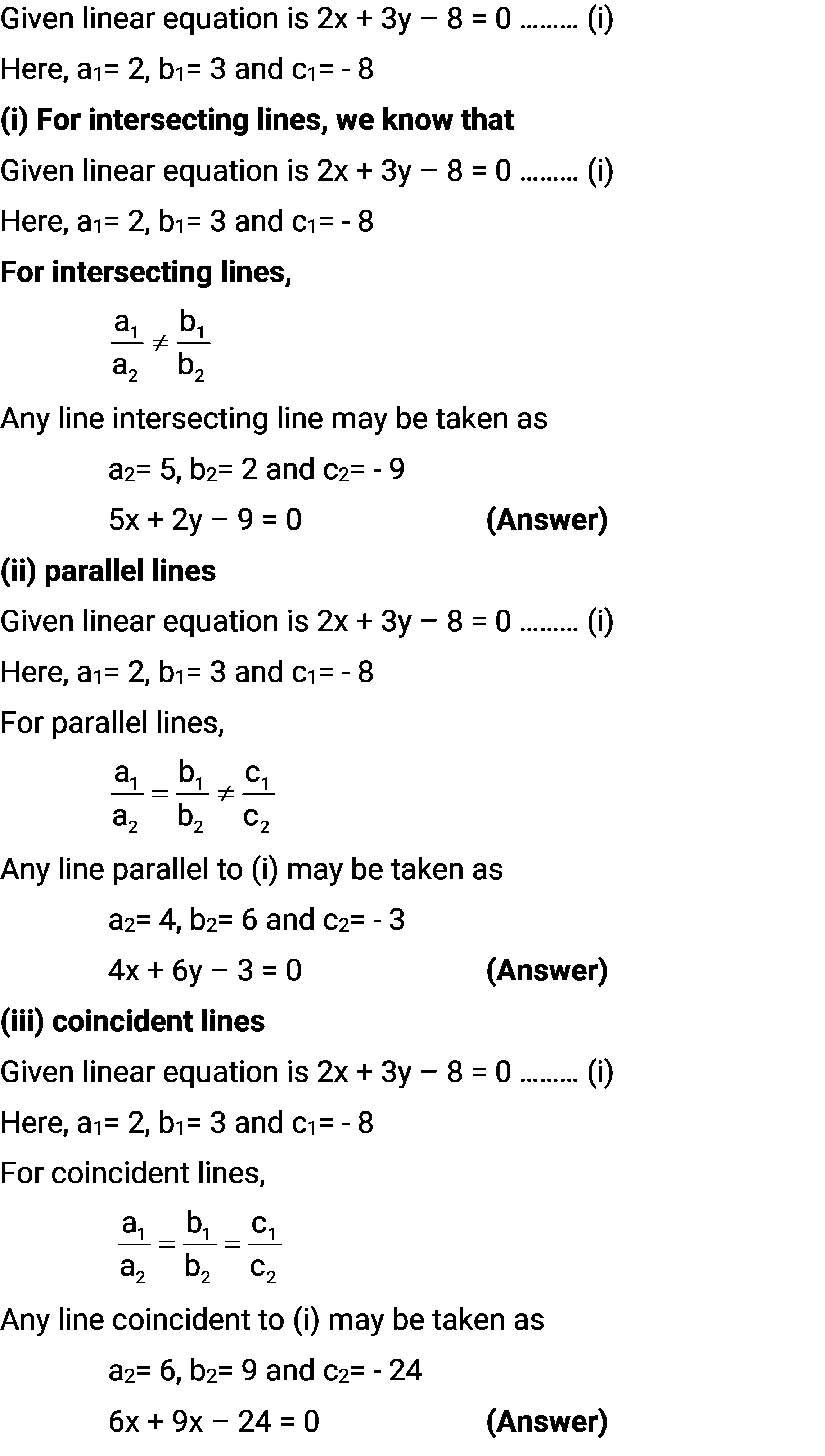
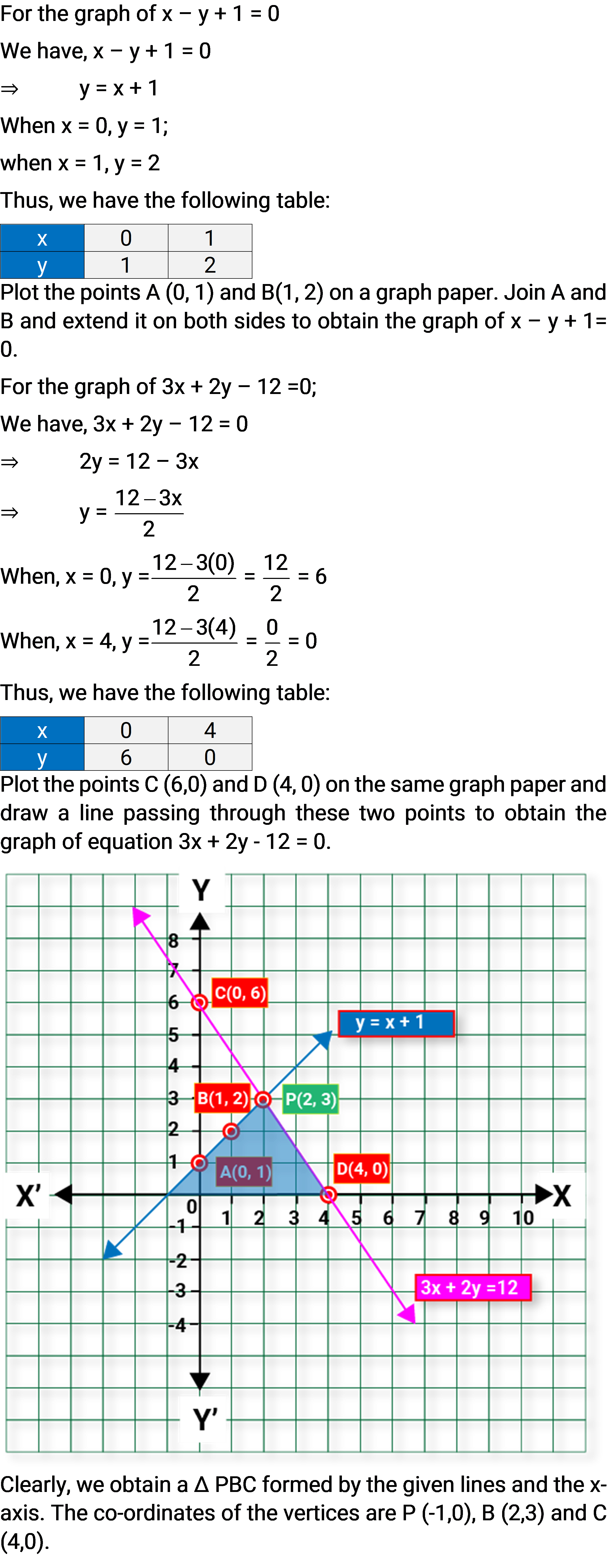
Q.7. Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Ans:
NCERT Solutions For Class 10, Maths, Chapter 3, Pair Of Linear Equations In Two Variables (All Exercises)
- Class 10, Maths, Chapter 4, Pair Of Linear Equations In Two Variables, Exercise 3.1
- Class 10, Maths, Chapter 4, Pair Of Linear Equations In Two Variables, Exercise 3.2
- Class 10, Maths, Chapter 4, Pair Of Linear Equations In Two Variables, Exercise 3.3
- Class 10, Maths, Chapter 4, Pair Of Linear Equations In Two Variables, Exercise 3.4
- Class 10, Maths, Chapter 4, Pair Of Linear Equations In Two Variables, Exercise 3.5
- Class 10, Maths, Chapter 4, Pair Of Linear Equations In Two Variables, Exercise 3.6

