Class 10, Maths, Chapter 5, Exercise 5.4 Solutions
Q.1. Which term of the AP : 121, 117, 113, . . ., is its first negative term? [Hint : Find n for an < 0]
Ans: Given AP is 121, 117, 113, …
a = 121, d = 117 – 121 = – 4
∵ an = a + (n – 1) d
an = 121 + (n – 1) x (- 4)
an = 121 – 4n + 4
an = 125 – 4n
For the first negative term
An < 0 = 125 – 4n < 0
⟹ 125 < 4n
⟹ $\frac{125}{4}$< n
⟹ $31\frac{1}{4}$ < n
n is an integer and n > . Hence, the first negative term is 32nd term.
Q.2. The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
Ans: Let the AP be a, (a + d), (a + 2d), (a + 3d)…..
Now, according to the question,
a3 + a7 = 6
∵ an = a + (n-1) d
⟹ (a + (3-1) d) + (a + (7-1) d) = 6
⟹ (a + 2d) + (a + 6d) = 6
⟹ 2a + 8d = 6
⟹ 2(a + 4d) = 6
⟹ a + 4d = 3
⟹ a = 3 – 4d ……… (i)
And, a3 x a7 = 8
⟹ (a + (3-1) d) x (a + (7-1) d) = 8
⟹ (a + 2d) x (a + 6d) = 8
From eq. (i)
⟹ [(3 – 4d) + 2d] x [(3 – 4d) + 6d] = 8
⟹ (3 – 2d) (3 +2d) = 8
⟹ 9 – 4d2 = 8
⟹ 4d2 = 9 – 8
⟹ d2 = $\frac{1}{4}={{\left( \frac{1}{2} \right)}^{2}}$
⟹ d = $\mp \frac{1}{2}$
Taking d = $+\frac{1}{2}$ , a = 3 –4 $\times \frac{1}{2}$=1 [Using (i)]
∴ S16 = $\frac{16}{2}\left[ \left( 2\times 1 \right)+\left( 16-1 \right)\times \frac{1}{2} \right]$
⟹ S16 = $8\left[ 2+\frac{15}{2} \right]=8\left[ \frac{4+15}{2} \right]=8\times \frac{19}{2}=76$
Taking d = $-\frac{1}{2}$, a = 3 – 4 $\times \left( -\frac{1}{2} \right)$ = 5 [Using (i)]
∴ S16 = $\frac{16}{2}\left[ \left( 2\times 5 \right)+\left( 16-1 \right)\times \left( -\frac{1}{2} \right) \right]$
⟹ S16 = $8\left[ 10-\frac{15}{2} \right]=8\left[ \frac{20-15}{2} \right]=8\times \frac{5}{2}=20$
Hence, the sum of first sixteen terms 20 or 76.
Q.3. A ladder has rungs 25 cm apart. (see Fig. 5.7). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are 2 $\frac{1}{2}$ m apart, what is the length of the wood required for the rungs? [Hint: Number of rungs = $\frac{250}{25}$+ 1]
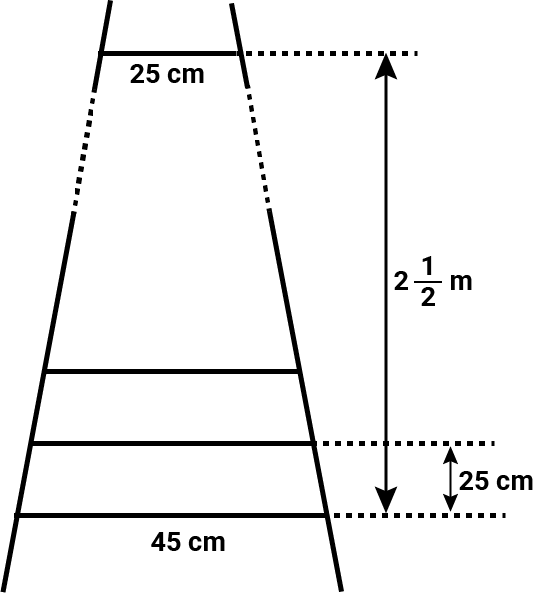
Ans: it is given that the rungs are 25 cm apart and the top and the bottom rungs are 2 $\frac{1}{2}$ m apart.
∴ Number of rungs, n = $\frac{2\frac{1}{2}\times 100\,\,cm}{25\,\,cm}+1=\frac{250\,\,cm}{25\,\,cm}+1=10+1=11$
So, there are 11 rungs
As the rungs decrease uniformly in length from 45 cm to 25 cm. it is in the form of AP.
Here, a = 45, last term (l) = 25 and n = 11 terms (= total rungs)
∴The length of the wood required for rungs = sum of 10 rungs
We know that, ${{S}_{n}}=\frac{n}{2}(a+l)$
${{S}_{11}}=\frac{11}{2}(45+25)$
${{S}_{11}}=\frac{11}{2}(70)=11\times 35=385\,\,cm$
Hence, the length of the wood required for the rungs is 385 cm.
Q.4. The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x. [Hint : Sx – 1 = S49 – Sx]
Ans:
Q.5. A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of $\frac{1}{4}$, and a tread of $\frac{1}{2}$m. (see Fig. 5.8). Calculate the total volume of concrete required to build the terrace. [Hint : Volume of concrete required to build the first step = $\frac{1}{4}\times \frac{1}{2}\times 50\,\,{{m}^{3}}$]
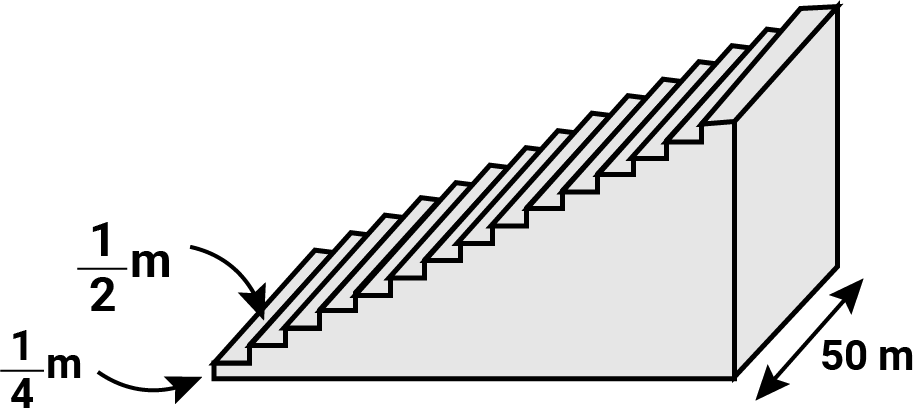
Ans:
