Class 10, Maths, Chapter 12, Exercise 12.1, Solutions
Q.1. The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Ans:
Let r be the radius of the circle whose circumference is equal to the sum of the circumference of two circle of radii 19 cm and 9 cm.
∴ 2πr1 + 2πr2 = 2πr
Diving by 2π, we get
⇒ $\frac{2\pi {{r}_{1}}}{2\pi }+\frac{2\pi {{r}_{2}}}{2\pi }=\frac{2\pi r}{2\pi }$
⇒ r1 + r2 = r or
⇒ r = r1 + r2
⇒ r = 19 + 9 = 28 cm (Ans)
Hence, the radius of the new circle is 28 cm
Q.2. The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Ans: Let r be the radius of the circle whose area is equal to the sum of the areas of the circles of radii 8 cm and 6 cm
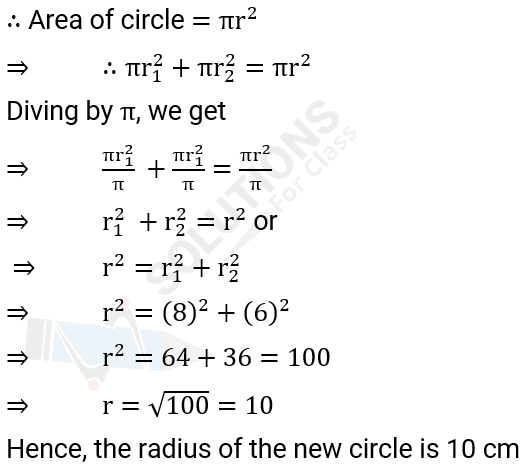
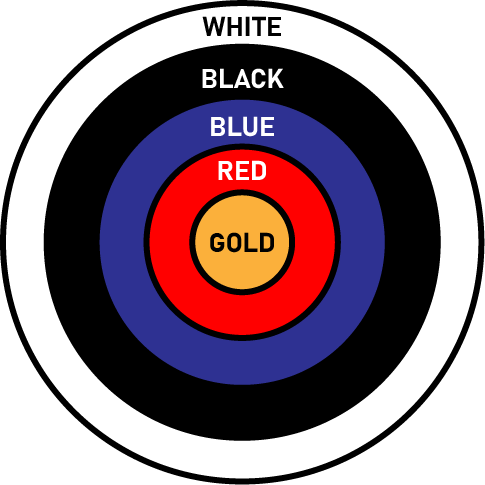
Q.3. Fig. 12.3 depicts an archery target marked with its five scoring regions from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Ans:
Diameter of Gold region = 21 cm (Given)
∴ Radius of Gold region, r1 = $\frac{21}{2}$ = 10.5 cm
Now, each of bands is 10.5 cm wide. Therefore, radius of another region:
Radius of Red region, r2 = 10.5 +10.5 = 21
Radius of Blue region, r3= 21 + 10.5 = 31.5
Radius of Black region, r4 = 31.5 + 10.5 = 42
Radius of White region, r5 = 42 + 10.5 = 52.5
Q.4. The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Ans: Diameter of wheel of car = 80 cm
∴ Radius of circle (wheel) = $\frac{80}{2}$= 40 cm
As we know that, circumference of circle is equal to 1 cycle or revolution.
Circumference of circle (wheel) = 2πr = 2π (40) = 80π cm
Speed = 66 km/hr
Speed (in meter/min) = 66 km/hr = 66,000 m / 60 min
Speed (in cm/min) = 6600 000 cm/hr
∵ 60 min requires to cover distance = 6600000 cm
∴ 1 min requires to cover distance = $\frac{6600000}{60}$ cm
∴ 10 min requires to cover distance = $\frac{6600000}{60}\times 10$ = 1100000 cm
Therefore, number of total revolutions =
$\frac{1100000\times 7}{2\times 22\times 4}=\frac{10000\times 7}{8\times 2}=\frac{8750}{2}$= 4375
Hence, the wheel of car makes 4375 revolutions in 10 min.
Q.5. Tick the correct answer in the following and justify your choice: If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(A) 2 units
(B) π units
(C) 4 units
(D) 7 units
Ans: (A) 2 units
Explanation: Here, perimeter of the circle = Area of a circle (Given)
⇒ 2πr = πr2 (r= radius)
⇒ 2r = r2 or
⇒ r = 2 units