
Table of Contents
ToggleClass 6, Maths, Chapter 3, Exercise 3.3 Solutions
Q.1. Using divisibility tests, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10 ; by 11 (say, yes or no):
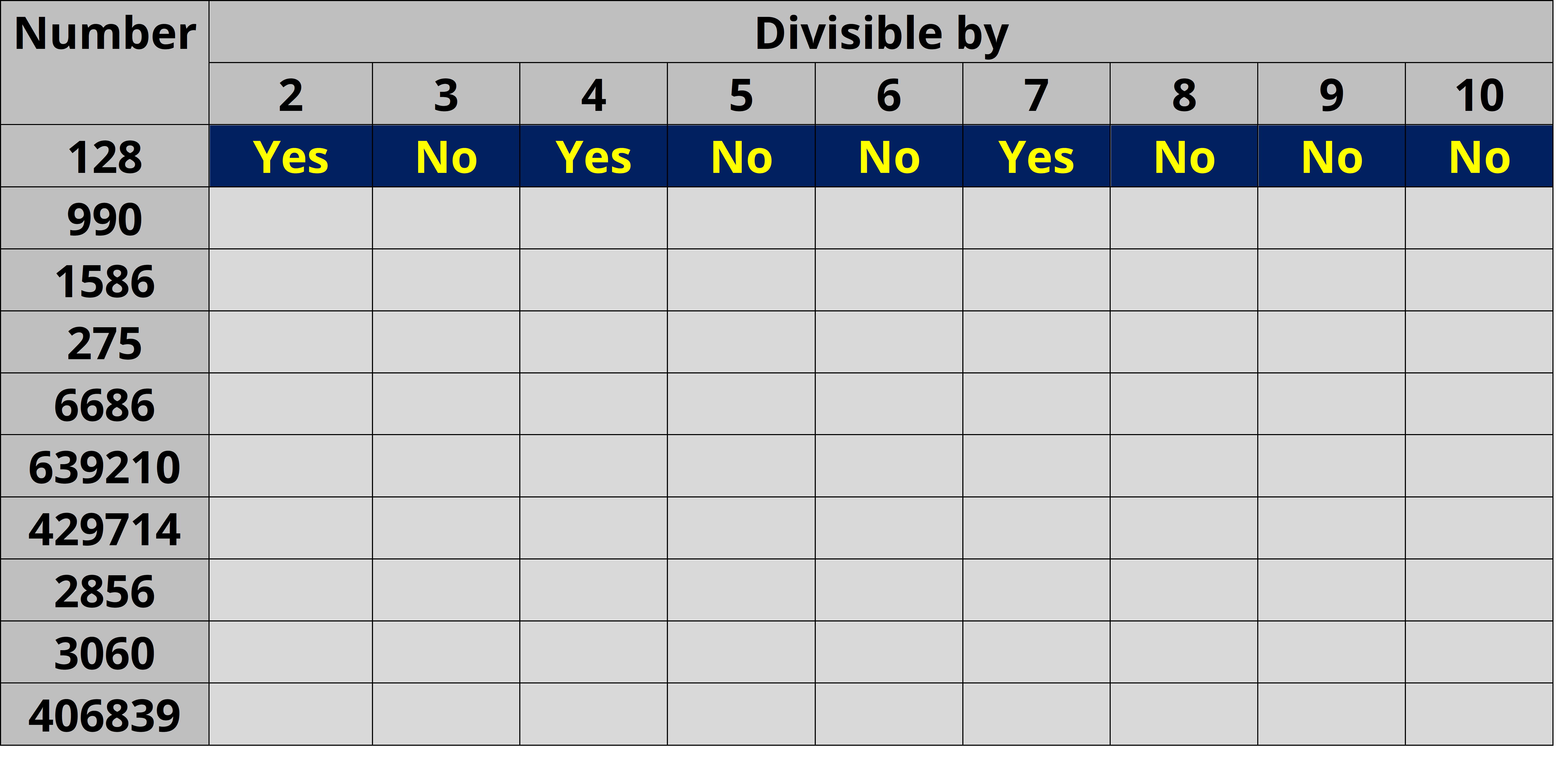
Ans:
Q.2. Using divisibility tests, determine which of the following numbers are divisible by 4; by 8:
(a) 572
(b) 726352
(c) 5500
(d) 6000
(e) 12159
(f) 14560
(g) 21084
(h) 31795072
(i) 1700
(j) 2150
Ans:

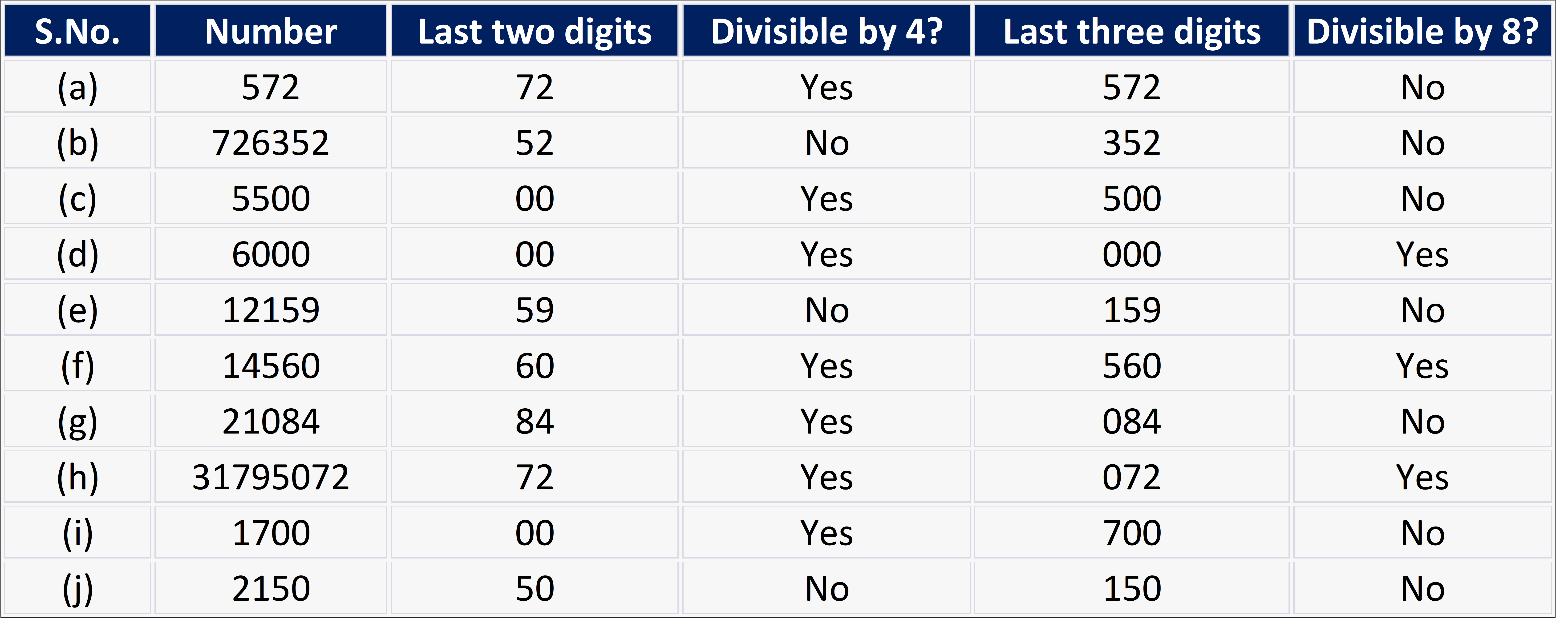
Alternatively,
(a) 572
In this case, the last two digits of 572 are 72, which is divisible by 4. Therefore, 572 is divisible by 4.
572 is not divisible by 8 as its last three digits i.e. 572 are not divisible by 8. Hence, 572 is not divisible by 8
(b) 726352
In this case, the last two digits of 726352 are 52 which is divisible by 4.
726352 is not divisible by 8 as its last three digits i.e. 352 are not divisible by 8. Hence, 726352 is not divisible by 8.
(c) 5500
In this case, the last two digits of 5500 are 00 which is divisible by 4. Hence, 5500 is also divisible by 4.
5500 is not divisible by 8 as its last three digits i.e. 500 are not divisible by 8. Hence, 5500 is not divisible by 8.
(d) 6000
6000 is divisible by 4 as its last two digits i.e. 00 are divisible by 4. Hence, 6000 is also divisible by 4.
6000 is divisible by 8 as its last three digits i.e. 000 are divisible by 8. Hence, 6000 is divisible by 8.
(e) 12159
12159 is not divisible by 4 as its last two digits i.e. 59 are not divisible by 4. Hence, 12159 is not divisible by 4.
12159 is not divisible by 8 as its last three digits i.e. 159 are not divisible by 8. Hence, 12159 is not divisible by 8.
(f) 14560
14560 is divisible by 4 as its last two digits i.e. 60 are divisible by 4. Hence, 14560 is also divisible by 4.
14560 is divisible by 8 as its last three digits i.e. 560 are divisible by 8. Hence, 14560 is divisible by 8.
(g) 21084
21084 is divisible by 4 as its last two digits i.e. 84 are divisible by 4. Hence, 21084 is also divisible by 4.
21084 is not divisible by 8 as its last three digits i.e. 084 are not divisible by 8. Hence, 21084 is not divisible by 8.
(h) 31795072
31795072 is divisible by 4 as its last two digits i.e. 72 are divisible by 4. Hence, 31795072 is also divisible by 4.
31795072 is divisible by 8 as its last three digits i.e. 072 are divisible by 8. Hence, 31795072 is divisible by 8.
(i) 1700
1700 is divisible by 4 as its last two digits i.e. 00 are divisible by 4. Hence, 1700 is also divisible by 4.
1700 is not divisible by 8 as its last three digits i.e. 700 are not divisible by 8. Hence, 1700 is not divisible by 8.
(j) 2150
2150 is not divisible by 4 as its last two digits i.e. 50 are not divisible by 4. Hence, 2150 is not divisible by 4.
2150 is not divisible by 8 as its last three digits i.e. 150 are not divisible by 8. Hence, 2150 is not divisible by 8.
Q.3. Using divisibility tests, determine which of following numbers are divisible by 6:
(a) 297144
(b) 1258
(c) 4335
(d) 61233
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 639210
(j) 17852
Ans:
Divisibility by 6 : if a number is divisible by 2 and 3 both then it is divisible by 6 also.
(a) 297144
Since the last digit of the number is 4, it is divisible by 2, so, the given number is divisible by 2
To check if a number is divisible by 3, we can add up its digits and see if the result is divisible by 3. In this case, 2+9+7+1+4+4=27, which is divisible by 3. Therefore, 297144 is divisible by 3.
Since 297144 is divisible by both 2 and 3, it is divisible by 6.
(b) 1258
Since the last digit of the number is 8, it is divisible by 2, so, the given number is divisible by 2
To check if a number is divisible by 3, we can add up its digits and see if the result is divisible by 3. In this case, 1+2+5+8 = 16, which is not divisible by 3. Therefore, 1258 is not divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, the number is not divisible by 6
(c) 4335
Since the last digit of the number is 5. Hence, the number is not divisible by 2.
By adding all the digits of the number, we get (4+3+3+5 =15) which is divisible by 3. Hence, the number is divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, the number is not divisible by 6
(d) 61233
Since the last digit of the number is 3. Hence, the number is not divisible by 2.
By adding all the digits of the number, we get (6+1+2+3+3=15) which is divisible by 3. Hence, the number is divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, the number is not divisible by 6.
(e) 901352
Since the last digit of the number is 2. Hence, the number is divisible by 2.
By adding all the digits of the number, we get (9+0+1+3+5+2=20) which is not divisible by 3. Hence, the number is not divisible by 3
Since, the number is not divisible by both 2 and 3. Therefore, the number is not divisible by 6.
(f) 438750
Since the last digit of the number is 0. Hence, the number is divisible by 2.
By adding all the digits of the number, we get (4+3+8+7+5+0 = 27) which is divisible by 3. Hence, the number is divisible by 3.
Since, the number is divisible by both 2 and 3. Therefore, the number is divisible by 6.
(g) 1790184
Since the last digit of the number is 4. Hence, the number is divisible by 2.
By adding all the digits of the number, we get (1+7+9+0+1+8+4=30) which is divisible by 3. Hence, the number is divisible by 3.
Since, the number is divisible by both 2 and 3. Therefore, the number is divisible by 6
(h) 12583
Since the last digit of the number is 3. Hence, the number is not divisible by 2.
By adding all the digits of the number, we get (1+2+5+8+3 = 19) which is not divisible by 3. Hence, the number is not divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, the number is not divisible by 6
(i) 639210
Since the last digit of the number is 0. Hence, the number is divisible by 2.
By adding all the digits of the number, we get (6+3+9+2+1+0=21) which is divisible by 3. Hence, the number is divisible by 3.
Since, the number is divisible by both 2 and 3. Therefore, the number is divisible by 6
(j) 17852
Since the last digit of the number is 2. Hence, the number is divisible by 2.
By adding all the digits of the number, we get (1+7+8+5+2=23) which is not divisible by 3. Hence, the number is not divisible by 3.
Since, the number is not divisible by both 2 and 3. Therefore, the number is not divisible by 6.
Alternatively:
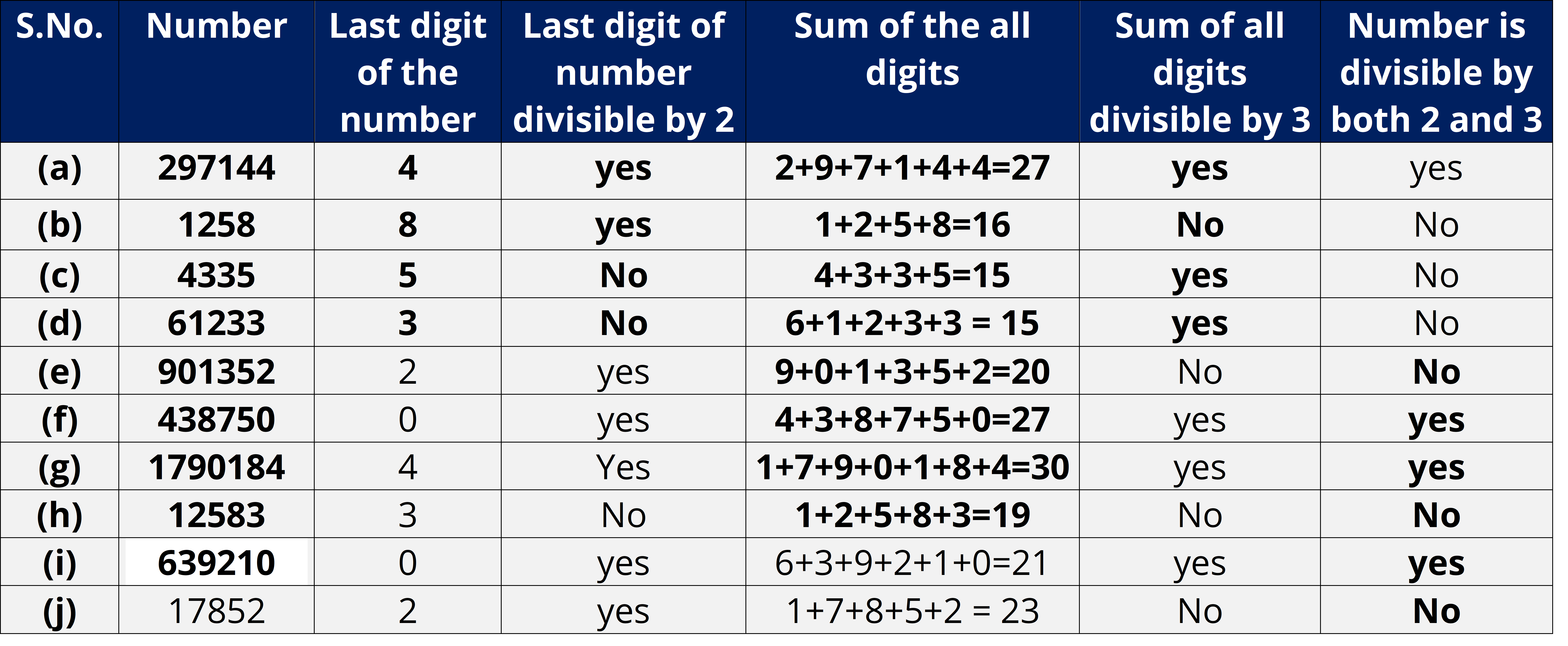
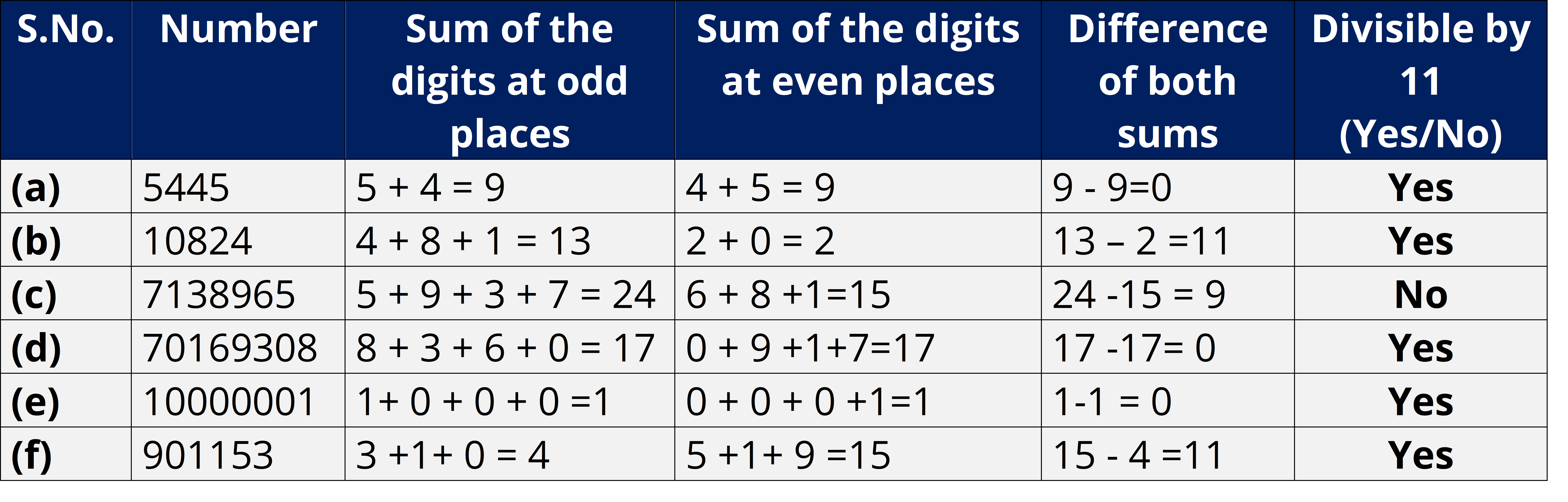
Q.4. Using divisibility tests, determine which of the following numbers are divisible by 11:
(a) 5445
(b) 10824
(c) 7138965
(d) 70169308
(e) 10000001
(f) 901153
Ans:
Divisibility by 11 : Find the difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) of the number. If the difference is either 0 or divisible by 11, then the number is divisible by 11.
Q.5. Write the smallest digit and the greatest digit in the blank space of each of the following numbers so that the number formed is divisible by 3 :
(a) __ 6724
(b) 4765 __ 2
Ans:
We know that a number is divisible by three if the sum of its digits is divisible by 3
(a) __ 6724
Let ‘x’ be placed here
= x6724
= x + 6+7+2+4
= x + 19
If x = 0, then 0 + 19 = 19 (Not possible)
If x = 1, then 1 + 19 = 20 (Not possible)
If x = 2, then 2 + 19 = 21 (Possible, smallest multiple of 3)
So, smallest number = 2
Now, to find greatest digit,
If x = (2+3), then, 5 + 19 = 24 (Possible)
If x = (2+3+3), then, 8 + 19 = 27 (Possible)
If x = (2+3+3+3), then, 11 + 19 = 30 (Not Possible)
Here, if we put 8, sum of digits will be 27 which is divisible by 3. Therefore, the number will be divisible by 3
Hence, the largest number is 8
(b) 4765 __ 2
Let ‘x’ be placed here
= 4765 x 2
= 4 + 7+ 6 + 5 + x + 2
= 24 + x
If x = 0, then 0 + 24 = 24 (possible)
So, smallest number = 0
Now, to find greatest digit,
If x = (0+3), then, 3 + 24 = 27 (Possible)
If x = (0+3+3), then, 6 + 24 = 30 (Possible)
If x = (0+3+3+3), then, 9 + 24 = 33 (Possible)
If x = (0+3+3+3+3), then, 12 + 24 = 36 (Not possible, we need only one digit number)
If we put 9, sum of its digits becomes 33. Since, 33 is divisible by 3. Therefore, the number will be divisible by 3
Hence, the greatest number is 9.
Q.6. Write a digit in the blank space of each of the following numbers so that the number formed is divisible by 11 :
(a) 92 __ 389
(b) 8 __ 9484
Ans:
We know that a number is divisible by 11, if the difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) of the number is either 0 or 11 or multiple of 11, then the number is divisible by 11.
(a) 92 __ 389
Let ‘x’ be placed here
= 96x389
Sum of its digits at odd places:
= 9 + x + 8
= 17 + x
Sum of its digits at even places:
= 2 + 3 + 9
= 14
Difference:
= 17 + x – 14
= 3 + x
The difference should be 0 or a multiple of 11, then the number is divisible by 11.
If 3 + x = 0 then a = -3 (it cannot be a negative)
If 3 + x = 11
3 + 8 = 11
∴ x = 8
Therefore, the required digit is 8
Let’s check it
We have, 17 + x – 14
Putting, x = 8
= 17 + 8 – 14
= 25 – 14
= 11
(b) 8 __ 9484
Let ‘x’ be placed here
= 8x9484
Sum of its digits at odd places:
= 8 + 9 + 8
= 25
Sum of its digits at even places:
= x + 4 + 4
= x + 8
Difference:
= 25 – (x + 8)
= 25 – x – 8
= 17 – x
The difference should be 0 or a multiple of 11, then the number is divisible by 11.
If 17 – x = 0 then x = 17
(Not possible, we need only one digit number)
If 17 – x = 11
17 – 6 = 11
∴ x = 6
Therefore, the required digit is 6.
Let’s check it
We have, = 25 – x – 8
Putting, x = 6
= 25 – 6 – 8
= 25 – 14
= 11
NCERT Solutions For Class 6 Maths, Chapter 3 Playing With Numbers (All Exercises)
Class 6, Maths, Chapter 3, Playing With Numbers
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.1
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.2
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.3 ← You are here
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.4
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.5
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.6
Class 6, Maths, Chapter 3, Playing With Numbers, Exercise 3.7

