Table of Contents
ToggleClass 8, Maths, Chapter 1, Exercise 1.1, Solutions
Q.1. Using appropriate properties find.
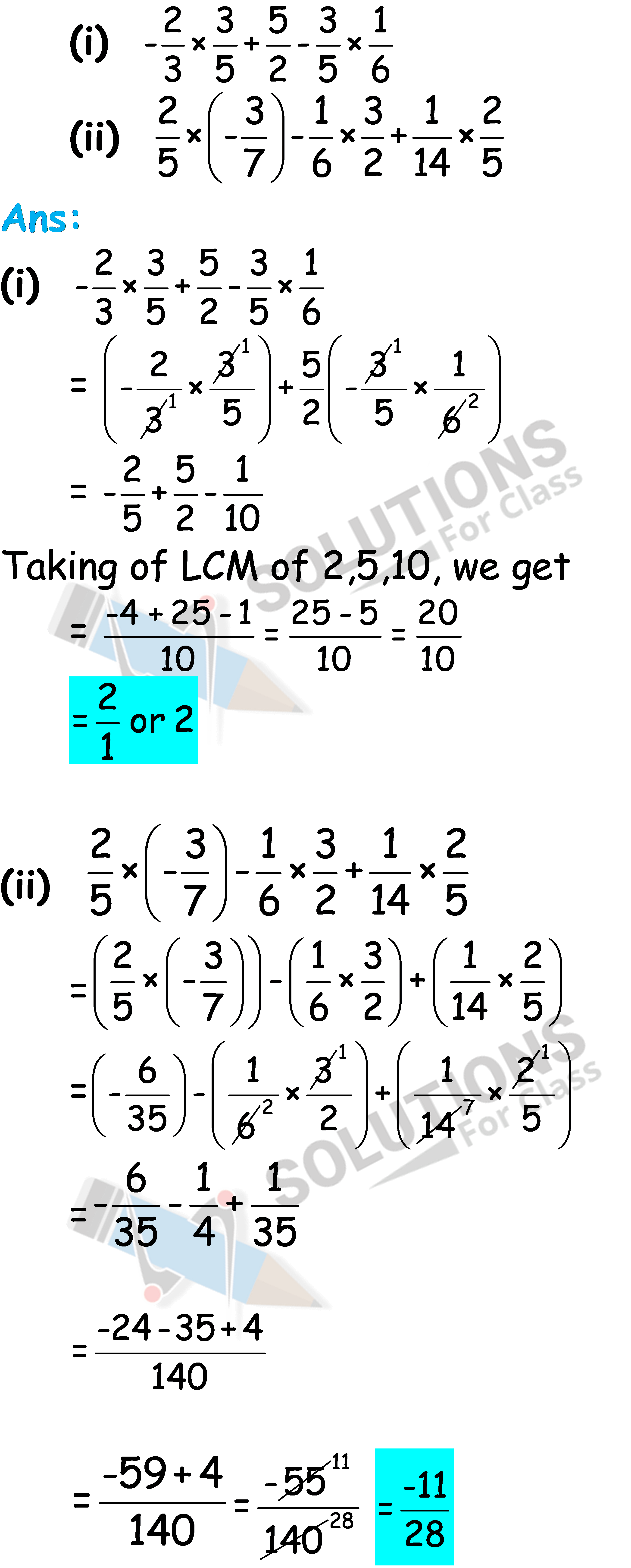
Q.2. Write the additive inverse of each of the following
(i) $\frac{2}{8}$
(ii) $\frac{-5}{9}$
(iii) $\frac{-6}{-5}$
(iv) $\frac{2}{-9}$
(v) $\frac{19}{-6}$
Ans:
(i) $\frac{2}{8}$
$\frac{2}{8}\Rightarrow \frac{-2}{8}$
(ii) $\frac{-5}{9}$
$\frac{-5}{9}\Rightarrow \frac{5}{9}$
(iii) $\frac{-6}{-5}$
$\frac{-6}{-5}\Rightarrow \frac{6}{5}$
(iv) $\frac{2}{-9}$
$\frac{2}{-9}\Rightarrow \frac{2}{9}$
(v) $\frac{19}{-6}$
$\frac{19}{-6}\Rightarrow \frac{19}{6}$
Q.3. Verify that – (– x) = x for.
(i) $x=\frac{11}{15}$
(ii) $x=-\frac{13}{17}$

Q.4. Find the multiplicative inverse of the following.
(i) -13
(ii) $\frac{-13}{19}$
(iii) $\frac{1}{5}$
(iv) $\frac{-5}{8}\times \frac{-3}{7}$
(v) $-1\times \frac{-2}{5}$
(vi) -1
Ans: We know that multiplicative inverse of x is $\frac{1}{x}$
(i) -13
$-13\Rightarrow \frac{1}{-13}$
(ii) $\frac{-13}{19}$
$\frac{-13}{19}\Rightarrow \frac{-19}{13}$
(iii) $\frac{1}{5}$
$\frac{1}{5}\Rightarrow \frac{5}{1}$
(iv) $\frac{-5}{8}\times \frac{-3}{7}$
$\frac{-5}{8}\times \frac{-3}{7}=\frac{-8}{5}\times \frac{-7}{3}=\frac{56}{15}$
Alternatively,
$\frac{\mathsf{-5}}{\mathsf{8}}\mathsf{\times }\frac{\mathsf{-3}}{\mathsf{7}}\mathsf{=}\frac{\mathsf{(-5)\times (-3)}}{\mathsf{8\times 7}}\mathsf{=}\frac{\mathsf{15}}{\mathsf{56}}\Rightarrow \frac{\mathsf{56}}{\mathsf{15}}$
(v) $-1\times \frac{-2}{5}$
$-1\times \frac{-2}{5}=\frac{\left( -1 \right)\times \left( -2 \right)}{5}=\frac{2}{5}\Rightarrow \frac{5}{2}$
(vi) -1
The multiplicative of -1 is -1.
-1 ⟹ -1
Q.5. Name the property under multiplication used in each of the following.
(i) $\frac{-4}{5}\times 1=1\times \frac{-4}{5}=-\frac{4}{5}$
(ii) $-\frac{13}{17}\times \frac{-2}{7}=\frac{-2}{7}\times \frac{-13}{17}$
(iii) $-\frac{19}{29}\times \frac{29}{-19}=1$
Ans:
(i) $\frac{-4}{5}\times 1=1\times \frac{-4}{5}=-\frac{4}{5}$
1 is the multiplicative identity.
(ii) $-\frac{13}{17}\times \frac{-2}{7}=\frac{-2}{7}\times \frac{-13}{17}$
since, a x b = b x a
therefore, it is commutatively.
(iii) $-\frac{19}{29}\times \frac{29}{-19}=1$
Multiplicative inverse.
Q.6. Multiply $\frac{6}{13}$ by the reciprocal of $\frac{-7}{16}$.

Q.7. Tell what property allows you to compute $\frac{1}{3}\times \left( 6\times \frac{4}{3} \right)\ $ as $\left( \frac{1}{3}\times 6 \right)\times \frac{4}{3}\ $.

Q.8. Is $\frac{8}{9}$ the multiplicative inverse of $-1\frac{1}{8}$ ? Why or why not?

Q.9. Is 0.3 the multiplicative inverse of $3\frac{1}{3}$.? Why or why not?

Q.10. Write.
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Ans:
(i) The rational number that does not have a reciprocal. = zero,
(ii) The rational numbers that are equal to their reciprocals. = 1, -1
(iii) The rational number that is equal to its negative. = 0
Q.11. Fill in the blanks.
(i) Zero has ________ reciprocal.
(ii) The numbers ________ and ________ are their own reciprocals
(iii) The reciprocal of – 5 is ________.
(iv) Reciprocal of $\frac{1}{x}$, where x ≠ 0 is ________.
(v) The product of two rational numbers is always a _______.
(vi) The reciprocal of a positive rational number is ________.
Ans:
(i) No
(ii) 1, -1
(iii) $-\frac{1}{5}$
(iv) x
(v) rational numbers
(vi) positive numbers.

