
Table of Contents
ToggleClass 9, Maths, Chapter 5, Exercise 5.1, Solutions
Q.1. Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
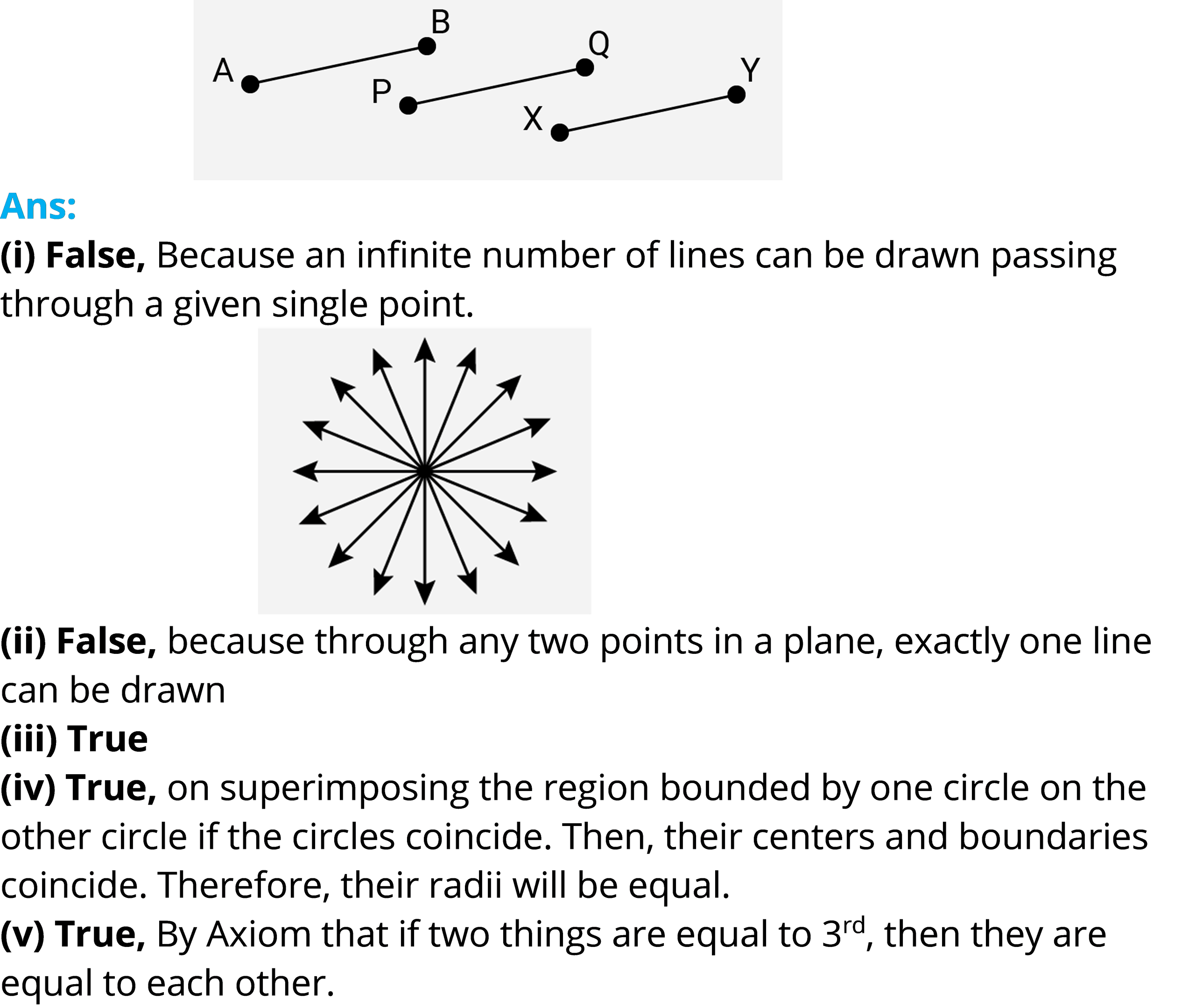
(v) In Figure, if AB = PQ and PQ = XY, then AB = XY.
Q.2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
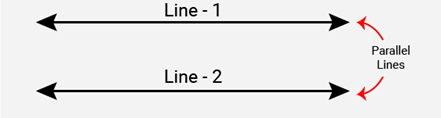
(i) Parallel lines
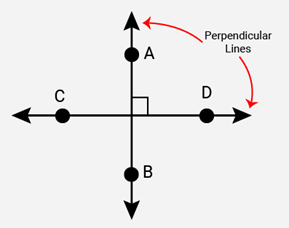
(ii) Perpendicular lines
(iii) Line segment
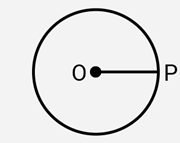
(iv) Radius of a circle
(v) Square
Ans: For the desired definition, we need the following terms:
(a) Point
(b) Line
(c) Plane
(d) Ray
(e) Angle
(f) Circle
(g) Quadrilateral
It is not possible to define first three precisely. However, a good idea of these concepts shall be given.
(a) Point: A small dot made by a sharp pencil on a sheet paper gives an idea about a point. A point has no dimension, it has only a position.
(b) Line: it is the straight and that it is extend in definitely in both the directions.
(c) Plane: The surface of a smooth wall or the surface of a sheet of paper are close example of a plane.
(d) Ray: A part of line l which has only one end-point A and contains the point B is called a ray AB.
(e) Angle: An angle is the union of two non-collinear rays with a common initial point.
(f) Circle: A circle is the set of all those points in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle.
(g) Quadrilateral: A closed figure made of four-line segment is called a quadrilateral
(i) Parallel Lines: Two lines are said to be parallel when
(a) They are not intersecting.
(b) They are coplanar and always maintain the same distance at every point. In figure, the two lines line – 1 and line – 2 are parallel.
(ii) Perpendicular Lines: Two lines AB and CD lying the same plane are said to be perpendicular, if they form a right angle. We write AB CD.Perpendicular lines intersect each other in a plane at right angles.
Lines and Angle terms need to be defined first.
(iii) Line segment: A line segment is a part of line. A line with end point is a line segment which cannot be extended any further.

It is named as $\overline{AB}$. AB and BA denote the same line segment.
Lines and Point terms need to be defined first.
(iv) Radius : The distance from the centre to a point on the circle boundary (Circumference) is called the radius of the circle. here in this figure, OP is the radius.
Circle and point terms need to be defined first.
(v) Square: A quadrilateral in which all the four angles are right angles (900) and four sides are equal is called a square.
Q.3. Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent?
Do they follow from Euclid’s postulates? Explain.
Ans: There are many undefined terms. They are consistent, because they deal with two different situations-
(i) Says that the given two points A and B, there is a point C lying on the line in between them;
(ii) Says that given A and B, we can take C not lying on the line through A and B.
These ‘postulates’ do not follow from Euclid’s postulates. They follow from axiom stated as “Given two distinct points, there is a unique line that passes through them”.
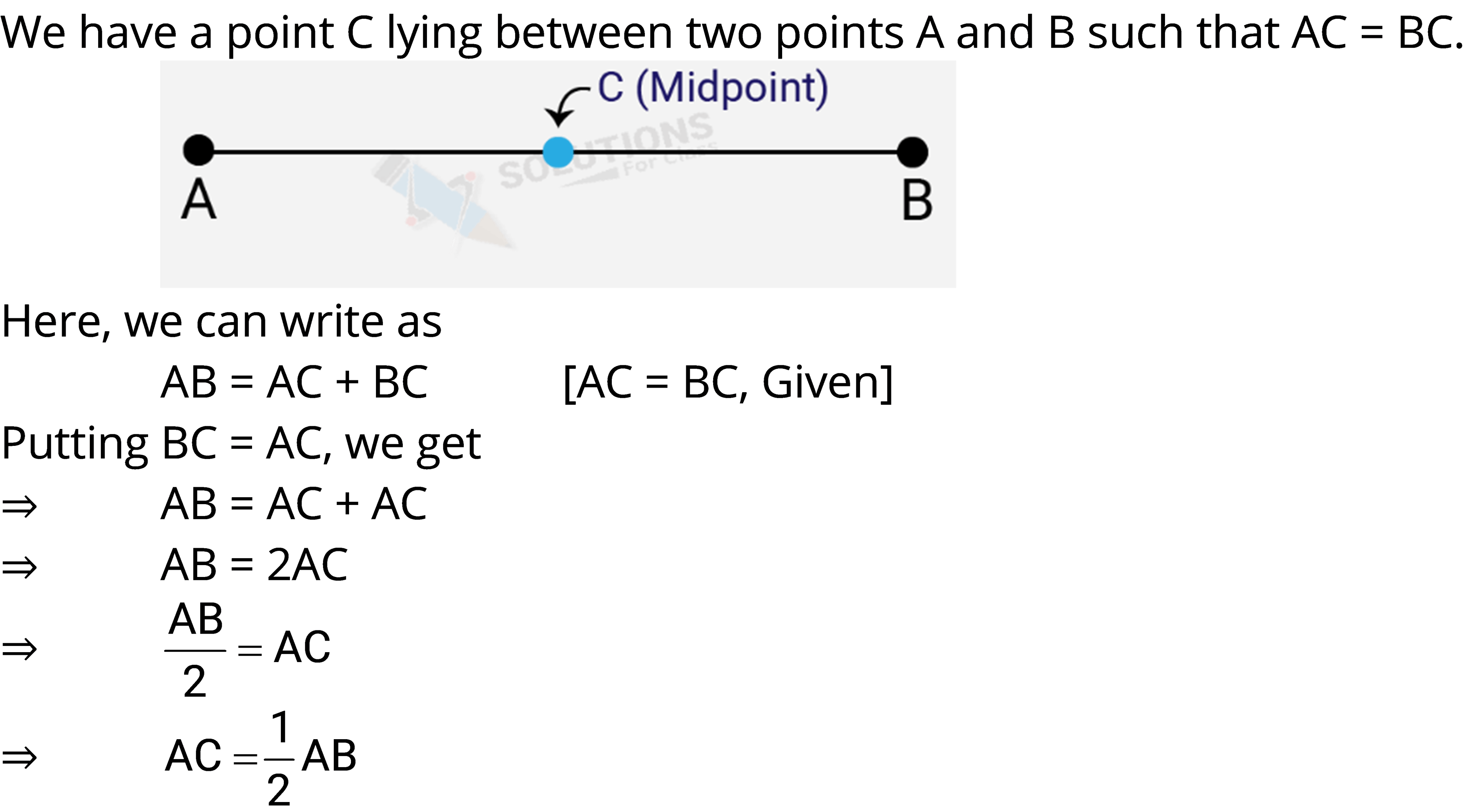
Q.4. If a point C lies between two points A and B such that AC = BC, then prove that $AC=\,\frac{1}{2}AB$. Explain by drawing the figure.
Ans:
Q.5. In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Ans:

Q.6. In Figure, if AC = BD, then prove that AB = CD.
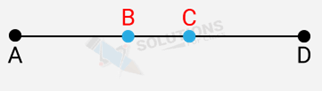
Ans: AC = BD ….(i) [Given]
Also, AC = AB + BC ….(ii) [Point B lies between A and C]
And, BD = BC + CD …..(iii) [Point C lies between B and D]
Substituting for AC and BD from (ii) and (iii) in (i), we get
AB + BC = BC + CD
AB + BC – BC = BC+CD – BC
AB = CD (Hence proved)
Q.7. Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
Ans: Axiom 5 in the list of Euclid’s axioms, is true for anything in any part of universe. because part is include in the whole and never greater than whole.

