NCERT Solution For Class 10, Maths, Chapter 8, Introduction To Trigonometry, Exercise 8.2 solutions are given below. Ex.8.2 deals study with trigonometric ratios of various angles and also you need to find justifications of each question.
Table of Contents
Toggle
Class 10, Maths, Chapter 8, Exercise 8.2, Solutions
Q.1. Evaluate the following :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60°
(iii) $\frac{\cos \,\,{{45}^{0}}}{\sec \,\,{{30}^{0}}+\cos ec\,\,{{30}^{0}}}$
(iv) $\frac{\sin \,{{30}^{0}}+\tan \,{{45}^{0}}-\cos ec\,{{60}^{0}}}{\sec \,{{30}^{0}}+\cos \,{{60}^{0}}+\cot \,{{45}^{0}}}$
(v) $\frac{5\,{{\cos }^{2}}\,\,{{60}^{0}}+4\,\,{{\sec }^{2}}\,{{30}^{0}}-{{\tan }^{2}}\,\,{{45}^{0}}}{{{\sin }^{2}}\,{{30}^{0}}+{{\cos }^{2}}\,{{30}^{0}}}$
Ans:
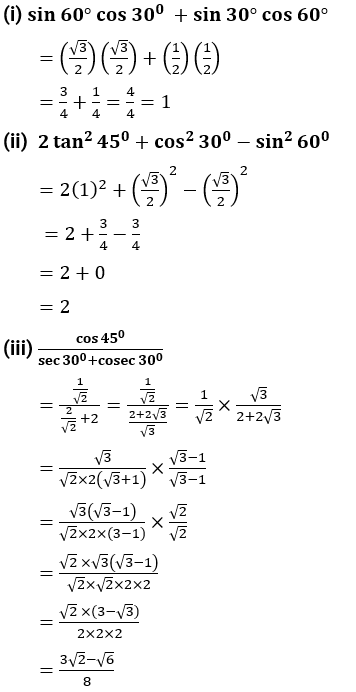
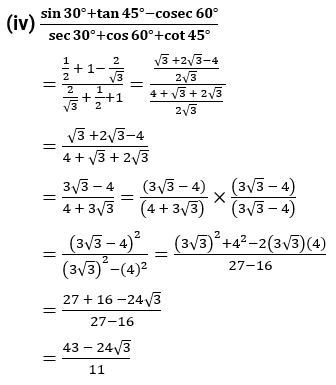
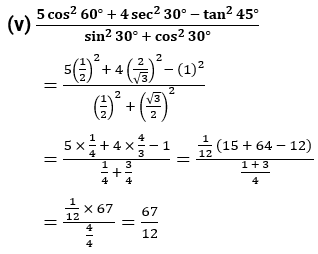
Q.2. Choose the correct option and justify your choice:
(i) $\frac{2\,\,\tan \,\,{{30}^{0}}}{1+{{\tan }^{2}}\,\,{{30}^{0}}}=$
(A) (B) cos 60° (C) tan 60° (D) sin 30°
(ii) $\frac{1-{{\tan }^{2}}\,\,{{45}^{0}}}{1+{{\tan }^{2}}\,\,{{45}^{0}}}=$
(A) tan 90° (B) 1 (C) sin 45° (D) 0
(iii) sin 2A = 2 sin A is true when A=
(A) 00 (B) 300 (C) 450 (d) 600
(iv) $\frac{2\,\,\tan \,\,{{30}^{0}}}{1-{{\tan }^{2}}\,\,{{30}^{0}}}=$
- cos 60° (B) sin 60° (C) tan 60° (D) sin 30°
Ans: (A)
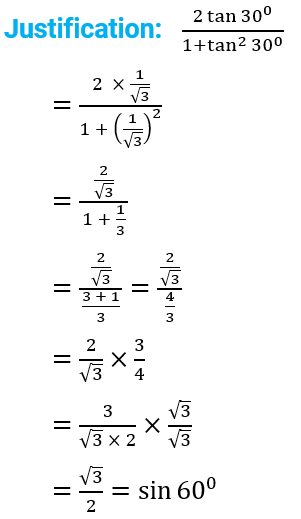
(ii) Correct option: (D)
Justification,
$\frac{1-{{\tan }^{2}}\,\,{{45}^{0}}}{1+{{\tan }^{2}}\,\,{{45}^{0}}}=\frac{1-1}{1+1}=\frac{0}{2}=0$
(iii) Correct option: (A)
Justification,
when A=00,
sin 2A = sin (2 × 00) = 0
And, 2 sin A = 2 sin 00 = (2 × 0) = 0
⇒ sin 2A = 2 sin A, when A=0
(iv) correct answer (C)
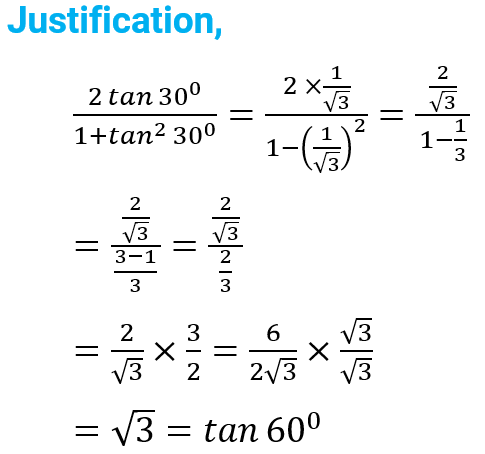
Q.3. If tan (A + B) = $\sqrt{3}$ and tan (A – B) = $\frac{1}{\sqrt{3}}$; 0° < A + B ≤ 90°; A > B, find A and B.
Ans:
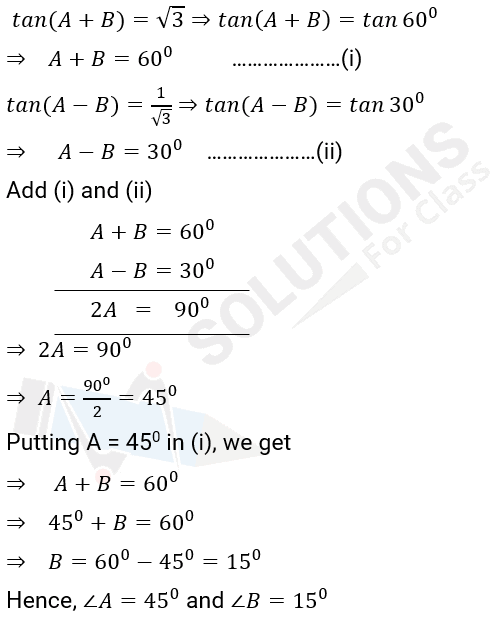
Q.4. State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
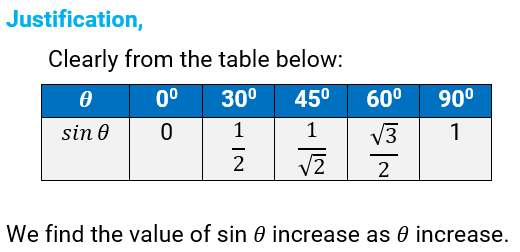
(ii) The value of sin θ increases as θ increases.
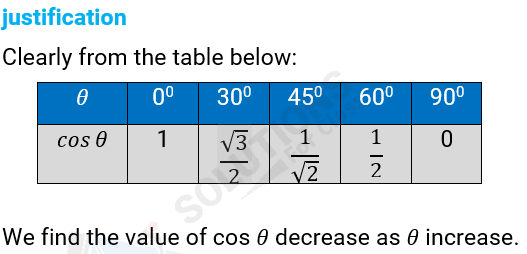
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Ans: (i) False
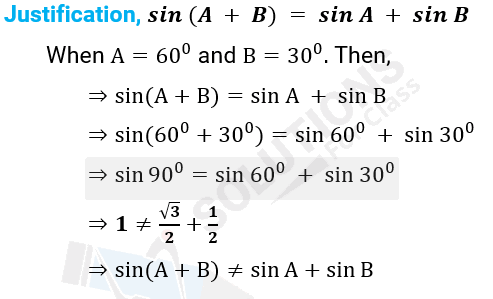
(ii) True
(iii) False
(iv) False
Justification,
⇒ sin 900 = cos 900
⇒ 1≠0
it is only true for $\theta -{{45}^{0}}\left( \sin \,\,{{45}^{0}}=\frac{1}{\sqrt{2}}=\cos \,\,{{45}^{0}} \right)$
(v) True
Justification,
⇒ cot 00 = 0 and cot 00 = $\frac{1}{\tan \,\,{{0}^{0}}}=\frac{1}{0}$ i.e., Not defined.

