NCERT Solution For Class 10, Maths, Quadratic Equations, Exercise 4.2 has some practical examples of quadratic equations. Chapter 4, Ex. 4.2 mainly has six questions to study.
Table of Contents
Toggle
Class 10, Maths, Chapter 4, Exercise 4.2 Solutions
Q.1. Find the roots of the following quadratic equations by factorization:
(i) x2 – 3x – 10 = 0
(ii) 2x2 + x – 6 = 0
(iii) $\sqrt{2}\,{{x}^{2}}+7x+5\sqrt{2}=0$
(iv) $2{{x}^{2}}-x+\frac{1}{8}=0$
(v) 100 x2 – 20x + 1 = 0
Ans:
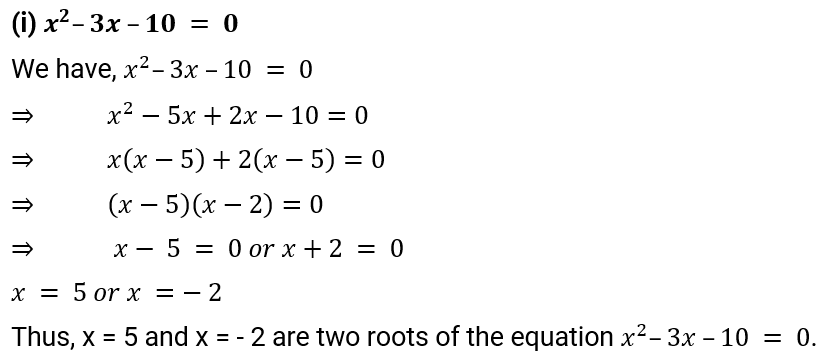
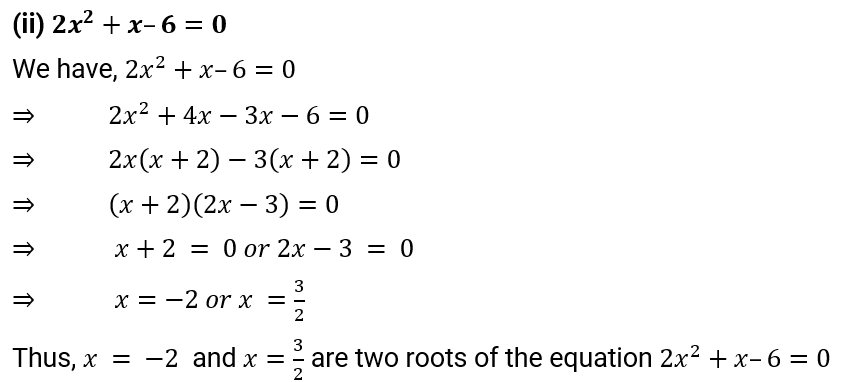
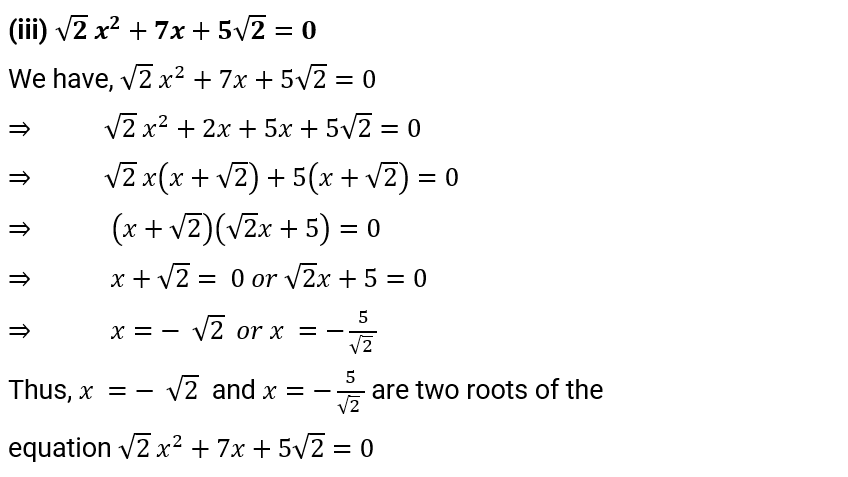
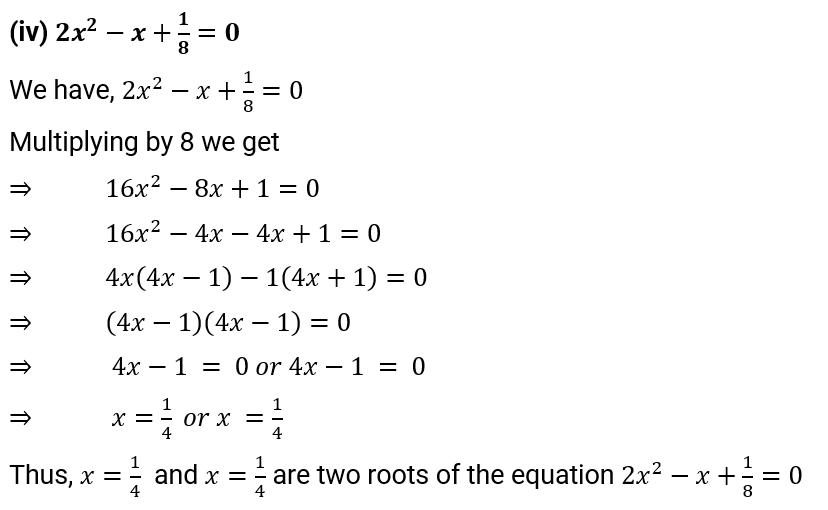
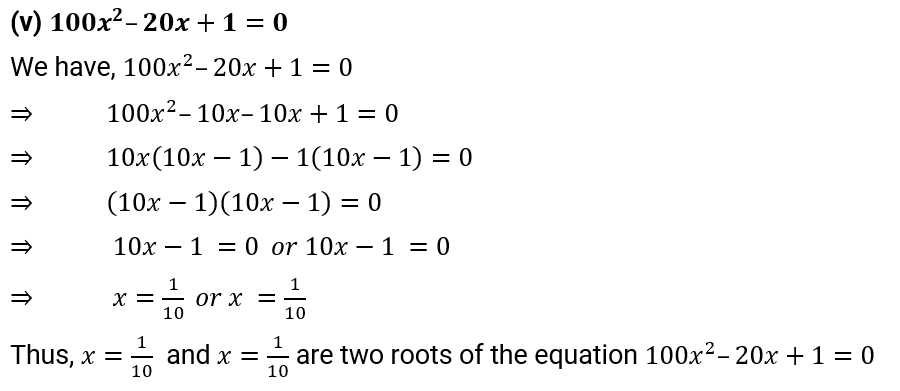
Q.2. Solve the problems given in Example 1.
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. We would like to find out the number of toys produced on that day
Ans:
(i) Let the number of marbles John had be x.
Then the number of marbles Jivanti had = 45 –x
When john lost 5 marbles, then number of marble left =x – 5
Therefore, the number of marbles left with Jivanti, when she lost 5 marbles =45 – x – 5 = 40–x
Therefore, their product =(x–5) (40–x)
= 40x–x2 – 200 + 5x
= –x2 + 45x – 200
Given the product of the number of marbles =124
So, –x2 + 45x – 200 = 124
i.e., –x2 + 45x – 324 = 0
i.e., x2 –45x + 324 = 0
Therefore, the number of marbles John had, satisfies the quadratic equation
⇒ x2–45x + 324 = 0
We have, x2 – 45x + 324 = 0
⇒ x2–9x – 36x + 324 = 0
⇒ x(x-9) – 36(x-9) = 0
⇒ (x-9) (x-36) = 0
⇒ x-9 = 0 or x – 36 =0
⇒ x = 9 or x = 36
Thus, x=9 and x=36 are two roots of the equation x2–45x + 324 = 0 or we can say that, John and Jivanti had 9 and 36 or 36 and 9 respectively.
(ii) Let the number of toys produced on that day be x.
Therefore, the cost of production (in ₹) of each toy that day = 55 – x
So, the total cost of production (in ₹) that day =x(55–x)
Therefore, x(55–x =750
i.e., 55x–x2=750
i.e., –x2 + 55x–750 =0
i.e., x2– 55x + 750 =0
Therefore, the number of toys produced that day satisfies the quadratic equation
⇒ x2–55x + 750 = 0
We have, x2–55x + 750 = 0
⇒ x2–30x – 25x + 750 = 0
⇒ x(x- 30) – 25(x-30)=0
⇒ (x-30) (x-25) = 0
⇒ x – 30 = 0 or x–25 =0
⇒ x = 30 or x =25
Thus, x=30 and x = 25 are two roots of the equation x2–55x + 750 = 0 or
We can say that
If the number of toys produced on that day be 30.
Then, the cost of production (in ₹) of each toy that day would be =55 –x=55-30=25 ₹
Or
If the number of toys produced on that day be 25.
Then, the cost of production (in ₹) of each toy that day would be =55 –x=55-25=35 ₹
Q.3. Find two numbers whose sum is 27 and product is 182.
Ans:

Q.4. Find two consecutive positive integers, sum of whose squares is 365.
Ans:

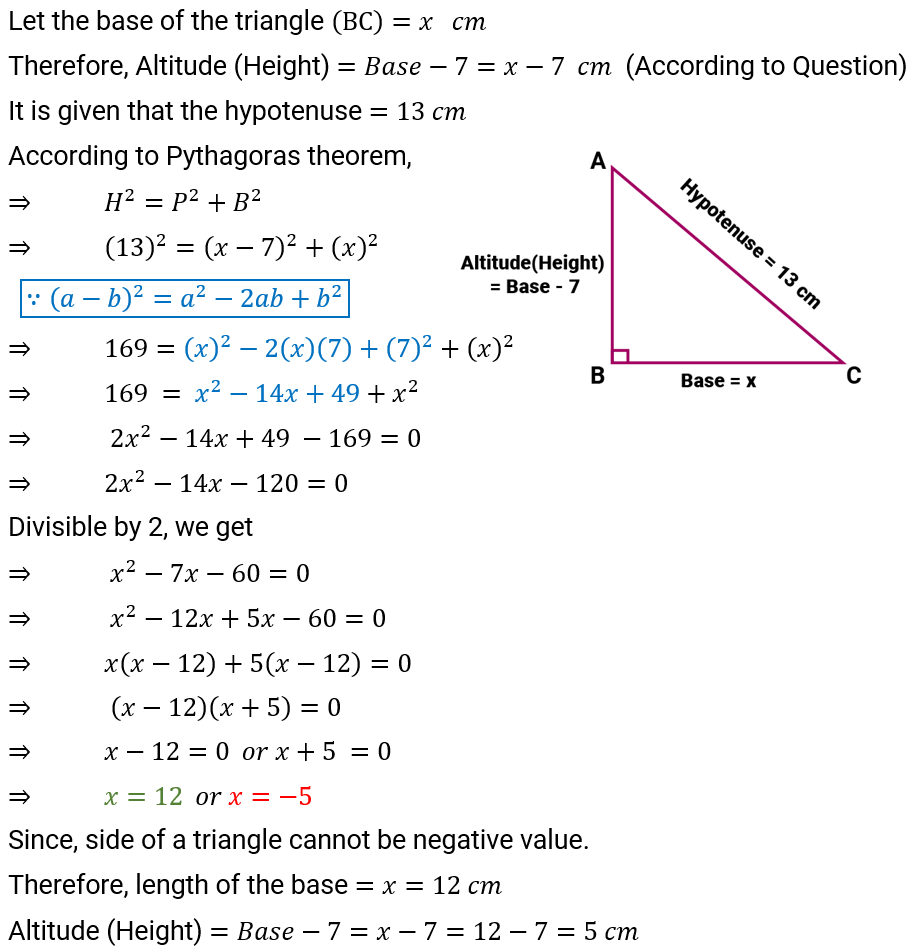
Q.5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Ans:
Q.6. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was ₹ 90, find the number of articles produced and the cost of each article.
Ans: Let the number of articles produced in a day = x
Then, cost of production of each article = ₹ (2x + 3) (according to question)
Total cost of production of each article on that day = ₹ 90
Therefore,
i.e., x(2x + 3) = 90
i.e., 2x2 + 3x = 90
i.e., 2x2 + 3x – 90 = 0
Therefore, the number of pottery articles produced that day satisfies the quadratic equation
⇒ 2x2 + 3x – 90 = 0
We have, 2x2 + 3x – 90 = 0
⇒ 2x2 – 12x + 15x – 90 = 0
⇒ 2x(x – 6) + 15(x – 6) = 0
⇒ (x – 6) (2x + 15) = 0
⇒ x – 6 = 0 or 2x + 15 = 0
⇒ x = 6 or x = $-\frac{15}{2}$
Since, the number of articles produced cannot be a negative number. Now, we can say that
If the number of articles produced on that day = x = 6
Then, the cost of production (in ₹) of each article that day would be =(2x + 3) = (2×6 + 3) = ₹ 15

